《2025年辽宁作业分层培优学案八年级数学上册北师大版》

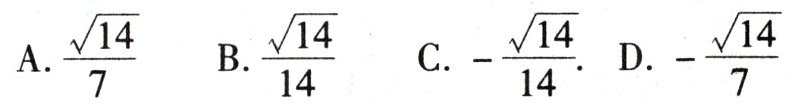
1. 计算$\sqrt{\dfrac{2}{7}}-\sqrt{\dfrac{1}{14}}$的结果是(B)

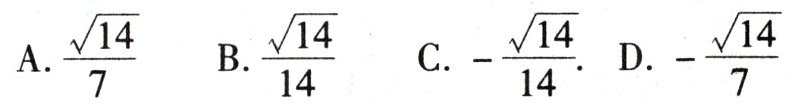
答案： B

2. (威海中考)计算：$\sqrt{12}-\sqrt{8}×\sqrt{6}=$$-2\sqrt{3}$。

答案： $-2\sqrt{3}$。

3. 计算：$\left(\dfrac{\sqrt{5}+1}{2}-1\right)×\dfrac{\sqrt{5}+1}{2}= $1。

答案： 1

4. 计算：
(1)$\sqrt{8}+4\sqrt{\dfrac{1}{2}}-\sqrt{18}$；
(2)$(4\sqrt{6}-3\sqrt{2})÷2\sqrt{2}$；
(3)(丹东期中)$(\sqrt{3}+\sqrt{2})(5 - 2\sqrt{6})$；
(4)$\sqrt{\dfrac{25}{2}}-\sqrt{12}×\left(\sqrt{24}+\sqrt{\dfrac{2}{3}}\right)$。

答案：
(1)
$\sqrt{8}+4\sqrt{\dfrac{1}{2}}-\sqrt{18}$
$=2\sqrt{2}+4×\frac{\sqrt{2}}{2}-3\sqrt{2}$
$=2\sqrt{2} + 2\sqrt{2}-3\sqrt{2}$
$=\sqrt{2}$
(2)
$(4\sqrt{6}-3\sqrt{2})÷2\sqrt{2}$
$=4\sqrt{6}÷2\sqrt{2}-3\sqrt{2}÷2\sqrt{2}$
$=2\sqrt{3}-\frac{3}{2}$
(3)
$(\sqrt{3}+\sqrt{2})(5 - 2\sqrt{6})$
$=5\sqrt{3}-2\sqrt{18}+5\sqrt{2}-2\sqrt{12}$
$=5\sqrt{3}-6\sqrt{2}+5\sqrt{2}-4\sqrt{3}$
$=\sqrt{3}-\sqrt{2}$
(4)
$\sqrt{\dfrac{25}{2}}-\sqrt{12}×(\sqrt{24}+\sqrt{\dfrac{2}{3}})$
$=\frac{5\sqrt{2}}{2}-2\sqrt{3}×(2\sqrt{6}+\frac{\sqrt{6}}{3})$
$=\frac{5\sqrt{2}}{2}-2\sqrt{3}×\frac{7\sqrt{6}}{3}$
$=\frac{5\sqrt{2}}{2}-\frac{14\sqrt{18}}{3}$
$=\frac{5\sqrt{2}}{2}-14\sqrt{2}$
$=-\frac{23\sqrt{2}}{2}$

5. 若$x = \sqrt{2}+1$,则代数式$x^{2}-2x + 2$的值为(C)
A.7
B.4
C.3
D.$3 - 2\sqrt{2}$

答案： C

6. (新考法·新定义阅读)对于任意的正数$m$,$n$定义运算※：$m※n= \begin{cases}\sqrt{m}-\sqrt{n}(m\geqslant n),\\\sqrt{m}+\sqrt{n}(m\lt n),\end{cases} 计算(3※2)×(8※12)$的结果为2。

答案： 2

7. 计算：
(1)$\dfrac{\sqrt{60}-\sqrt{15}}{\sqrt{3}}-3\sqrt{\dfrac{1}{5}}$；

(2)$\sqrt{27}-15\sqrt{\dfrac{1}{3}}+\dfrac{1}{4}\sqrt{48}$；
(3)(沈阳沈河区期末)$\left(\sqrt{\dfrac{9}{2}}-\dfrac{\sqrt{98}}{3}\right)÷\sqrt{2}+\dfrac{1}{3}$；
(4)$(\sqrt{6}-3)^{2}+\sqrt{24}-6\sqrt{\dfrac{8}{3}}$；
(5)$(\sqrt{3}-2)^{2026}×(\sqrt{3}+2)^{2027}$。

答案：
(1)
$\begin{aligned}&\frac{\sqrt{60}-\sqrt{15}}{\sqrt{3}}-3\sqrt{\frac{1}{5}}\\=&\frac{\sqrt{60}}{\sqrt{3}}-\frac{\sqrt{15}}{\sqrt{3}}-3×\frac{\sqrt{5}}{5}\\=&\sqrt{20}-\sqrt{5}-\frac{3\sqrt{5}}{5}\\=&2\sqrt{5}-\sqrt{5}-\frac{3\sqrt{5}}{5}\\=&\sqrt{5}-\frac{3\sqrt{5}}{5}\\=&\frac{5\sqrt{5}}{5}-\frac{3\sqrt{5}}{5}\\=&\frac{2\sqrt{5}}{5}\end{aligned}$
(2)
$\begin{aligned}&\sqrt{27}-15\sqrt{\frac{1}{3}}+\frac{1}{4}\sqrt{48}\\=&3\sqrt{3}-15×\frac{\sqrt{3}}{3}+\frac{1}{4}×4\sqrt{3}\\=&3\sqrt{3}-5\sqrt{3}+\sqrt{3}\\=&(3-5+1)\sqrt{3}\\=&-\sqrt{3}\end{aligned}$
(3)
$\begin{aligned}&\left(\sqrt{\frac{9}{2}}-\frac{\sqrt{98}}{3}\right)÷\sqrt{2}+\frac{1}{3}\\=&\left(\frac{3\sqrt{2}}{2}-\frac{7\sqrt{2}}{3}\right)×\frac{1}{\sqrt{2}}+\frac{1}{3}\\=&\frac{3\sqrt{2}}{2}×\frac{1}{\sqrt{2}}-\frac{7\sqrt{2}}{3}×\frac{1}{\sqrt{2}}+\frac{1}{3}\\=&\frac{3}{2}-\frac{7}{3}+\frac{1}{3}\\=&\frac{3}{2}-\left(\frac{7}{3}-\frac{1}{3}\right)\\=&\frac{3}{2}-2\\=&-\frac{1}{2}\end{aligned}$
(4)
$\begin{aligned}&(\sqrt{6}-3)^{2}+\sqrt{24}-6\sqrt{\frac{8}{3}}\\=&6 - 6\sqrt{6}+9 + 2\sqrt{6}-6×\frac{2\sqrt{6}}{3}\\=&15 - 6\sqrt{6}+2\sqrt{6}-4\sqrt{6}\\=&15-(6\sqrt{6}-2\sqrt{6}+4\sqrt{6})\\=&15 - 8\sqrt{6}\end{aligned}$
(5)
$\begin{aligned}&(\sqrt{3}-2)^{2026}×(\sqrt{3}+2)^{2027}\\=&[(\sqrt{3}-2)(\sqrt{3}+2)]^{2026}×(\sqrt{3}+2)\\=&(3 - 4)^{2026}×(\sqrt{3}+2)\\=&(-1)^{2026}×(\sqrt{3}+2)\\=&1×(\sqrt{3}+2)\\=&\sqrt{3}+2\end{aligned}$