《2025年辽宁作业分层培优学案八年级数学上册北师大版》

11. 勾股定理最早出现在商高的《周髀算经》:“勾广三,股修四,经隅五”. 观察下列勾股数:3,4,5;5,12,13;7,24,25;…,这类勾股数的特点是:勾为奇数,弦与股相差为1. 柏拉图研究了勾为偶数,弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;…,若此类勾股数的勾为2m(m ≥ 3,m为正整数),则其弦是$m^{2}+1$.(结果用含m的式子表示)

答案： $m^{2}+1$

12. 如图,在△ABC中,AD ⊥ BC,垂足为D. 如果AD = 6,BD = 9,CD = 4,那么∠BAC是直角吗? 请说明理由.

答案： 因为$AD \perp BC$，$AD = 6$，$BD = 9$，
根据勾股定理可得：
$AB=\sqrt{AD^{2} + BD^{2}}=\sqrt{6^{2}+9^{2}}=\sqrt{36 + 81}=\sqrt{117}$。
因为$AD \perp BC$，$AD = 6$，$CD = 4$，
根据勾股定理可得：
$AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{6^{2}+4^{2}}=\sqrt{36 + 16}=\sqrt{52}$。
$BC=BD + CD=9 + 4 = 13$。
因为$AB^{2}+AC^{2}=117 + 52=169$，$BC^{2}=13^{2}=169$，
所以$AB^{2}+AC^{2}=BC^{2}$。
根据勾股定理的逆定理，可知$\triangle ABC$是直角三角形，且$\angle BAC = 90^{\circ}$。
故$\angle BAC$是直角。

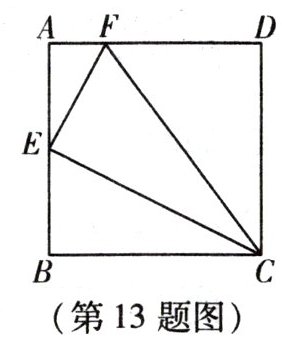
13. 如图,在正方形ABCD中,E为AB的中点,F是AD上一点,且$ AF = \frac{1}{4}AD $,试说明:△FEC是直角三角形.

答案： 设正方形ABCD的边长为$4a$。
$\because E$是AB中点，
$\therefore AE = BE = \frac{1}{2} × 4a = 2a$。
$\because AF = \frac{1}{4}AD$，
$\therefore AF = a$，$DF = 3a$。
在$Rt\triangle AEF$中，
根据勾股定理，$EF^{2} = AE^{2} + AF^{2}=(2a)^{2} + a^{2} = 5a^{2}$。
在$Rt\triangle BEC$中，
根据勾股定理，$EC^{2} = BE^{2} + BC^{2}=(2a)^{2} + (4a)^{2} = 20a^{2}$。
在$Rt\triangle DCF$中，
根据勾股定理，$FC^{2}=DF^{2}+DC^{2}=(3a)^{2} + (4a)^{2} = 25a^{2}$。
$\because EF^{2}+EC^{2}=5a^{2}+20a^{2}=25a^{2}=FC^{2}$。
根据勾股定理的逆定理，$\triangle FEC$是直角三角形。

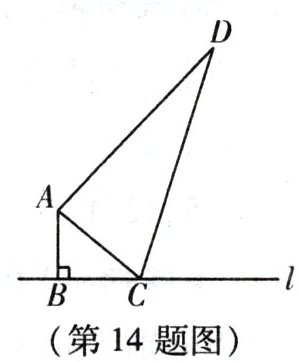
14. 如图,在△ABC中,∠ABC = 90°,AB = 6cm,AD = 24cm,BC与CD的长度之和为34cm,其中点C是直线l上的一个动点,请你探究当点C离点B多远时,△ACD是以CD为斜边的直角三角形.

答案： 设$BC = xcm$，则$CD =(34 - x)cm$。
在$Rt\triangle ABC$中，根据勾股定理$AC^{2}=AB^{2}+BC^{2}$，已知$AB = 6cm$，$BC = xcm$，可得$AC^{2}=36 + x^{2}$。
在$\triangle ACD$中，$AD = 24cm$，$CD=(34 - x)cm$，因为$\triangle ACD$是以$CD$为斜边的直角三角形，根据勾股定理$AC^{2}+AD^{2}=CD^{2}$。
把$AC^{2}=36 + x^{2}$，$AD = 24$，$CD = 34 - x$代入$AC^{2}+AD^{2}=CD^{2}$可得：
$36+x^{2}+24^{2}=(34 - x)^{2}$
$36+x^{2}+576 = 1156-68x+x^{2}$
$x^{2}-x^{2}+68x=1156 - 36 - 576$
$68x = 544$
$x = 8$
所以当点$C$离点$B$ $8cm$时，$\triangle ACD$是以$CD$为斜边的直角三角形。

15. (新考法·新定义阅读)定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
(1)已知M,N把线段AB分割成AM,MN,NB,若AM = 1.5,MN = 2.5,NB = 2,则点M,N是线段AB的勾股分割点吗? 请说明理由.
(2)已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB = 24,AM = 6,求NB的长.

答案：
(1)
点$M$，$N$是线段$AB$的勾股分割点。
理由：因为$AM = 1.5$，$MN = 2.5$，$NB = 2$，$AM^{2}+NB^{2}=1.5^{2}+2^{2}=2.25 + 4=6.25$，$MN^{2}=2.5^{2}=6.25$，所以$AM^{2}+NB^{2}=MN^{2}$，以$AM$，$MN$，$NB$为边的三角形是直角三角形，则点$M$，$N$是线段$AB$的勾股分割点。
(2)
设$NB=x$，则$MN = 24 - 6 - x=18 - x$。
因为$AM$为直角边，当$MN$为斜边时，$AM^{2}+NB^{2}=MN^{2}$，即$6^{2}+x^{2}=(18 - x)^{2}$，
$36+x^{2}=324-36x+x^{2}$，
$36x=324 - 36$，
$36x=288$，
$x = 8$。
当$NB$为斜边时，$AM^{2}+MN^{2}=NB^{2}$，即$6^{2}+(18 - x)^{2}=x^{2}$，
$36+324-36x+x^{2}=x^{2}$，
$36x=360$，
$x = 10$。
综上，$NB$的长为$8$或$10$。