《2025年辽宁作业分层培优学案八年级数学上册北师大版》

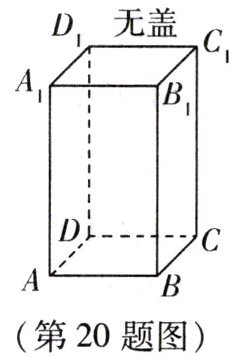
20. (7 分)如图,长方体的棱长 $ AB = BC = 6 $cm,$ AA_1 = 14 $cm,假设昆虫甲从盒内顶点 $ C_1 $ 开始以 1cm/s 的速度在盒子的内部沿棱 $ C_1C $ 向下爬行,同时昆虫乙从盒内顶点 $ A $ 以相同的速度在盒内壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？

答案： 解：
设昆虫乙捕捉到昆虫甲所需时间为 $ t $ 秒。此时昆虫甲从 $ C_1 $ 沿棱 $ C_1C $ 向下爬行 $ t \, cm $，到达点 $ P $，则 $ PC_1 = t \, cm $，$ PC = (14 - t) \, cm $（$ C_1C = 14 \, cm $）。昆虫乙从 $ A $ 点出发，在侧面爬行 $ t \, cm $ 到达点 $ P $。
关键步骤：
1. 侧面展开：将长方体的前面 $ ABB_1A_1 $ 与右面 $ BCC_1B_1 $ 展开成平面，形成一个长为 $ AB + BC = 6 + 6 = 12 \, cm $、高为 $ 14 \, cm $ 的长方形。
2. 最短路径计算：在展开平面中，$ A $ 到 $ P $ 的最短路径为直线距离。此时 $ A $ 点坐标为 $ (0,0) $，$ P $ 点坐标为 $ (12, 14 - t) $（$ P $ 在棱 $ C_1C $ 上，竖坐标为 $ 14 - t $）。
3. 勾股定理列方程：
由 $ AP = t $，得：
$ \sqrt{12^2 + (14 - t)^2} = t $
4. 解方程：
平方得：$ 12^2 + (14 - t)^2 = t^2 $
展开：$ 144 + 196 - 28t + t^2 = t^2 $
化简：$ 340 - 28t = 0 $
解得：$ t = \frac{340}{28} = \frac{85}{7} $
结论：
昆虫乙至少需要 $ \frac{85}{7} \, s $（即 $ 12\frac{1}{7} \, s $）才能捕捉到昆虫甲。
$\boxed{\dfrac{85}{7}}$

21. (10 分)(沈阳浑南区期末)如图,已知等腰三角形 $ ABC $ 中,$ AB = AC $,$ BC = 20 $cm,$ D $ 是边 $ AB $ 上一点,且 $ CD = 16 $cm,$ BD = 12 $cm.
(1) 求 $ AD $ 的长；
(2) 求 $ \triangle ABC $ 中 $ BC $ 边上的高.

答案：
(1) $ \frac{14}{3} \, cm $；
(2) $ \frac{40}{3} \, cm $。