第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
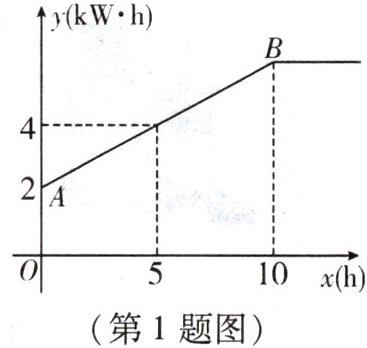
1. 太阳能光伏板是将太阳能转化为电能,并将电能储存起来的装置.某市政部门计划在路灯上安装一种智能太阳能光伏板,已知该太阳能光伏板某日的发电量 $ y $ (单位:$ kW \cdot h $) 与日照时间 $ x $ (单位:$ h $) 之间的关系如图所示. (假设早上 $ 8:00 $ 开始有光照)
(1) 求 $ AB $ 段 $ y $ 与 $ x $ 之间的函数表达式;
(2) 该市政部门规定每日 $ 18:00 $ (即日照 $ 10h $ 后) 打开路灯,次日的 $ 6:00 $ 关闭路灯,若路灯亮灯后每小时的耗电量为 $ 0.35kW \cdot h $,试判断该太阳能光伏板当日提供的电量能否使路灯达到该市政部门规定的亮灯时间. (忽略其他因素对电能储存及消耗的影响)
(1) 求 $ AB $ 段 $ y $ 与 $ x $ 之间的函数表达式;
(2) 该市政部门规定每日 $ 18:00 $ (即日照 $ 10h $ 后) 打开路灯,次日的 $ 6:00 $ 关闭路灯,若路灯亮灯后每小时的耗电量为 $ 0.35kW \cdot h $,试判断该太阳能光伏板当日提供的电量能否使路灯达到该市政部门规定的亮灯时间. (忽略其他因素对电能储存及消耗的影响)

答案:
(1)设$AB$段$y$与$x$之间的函数表达式为$y = kx + b$。
由图象可知$A(0,2)$,$B(10,6)$($10$小时对应$B$点纵坐标$4 + 2 = 6$),把$A(0,2)$,$B(10,6)$代入$y = kx + b$得:
$\begin{cases}b = 2\\10k + b = 6\end{cases}$
将$b = 2$代入$10k + b = 6$得$10k+2 = 6$,$10k = 4$,解得$k=\frac{2}{5}$。
所以$AB$段$y$与$x$之间的函数表达式为$y=\frac{2}{5}x + 2(0\leqslant x\leqslant10)$。
(2)当$x = 10$时,$y=\frac{2}{5}×10 + 2=6$,即当日发电量为$6kW\cdot h$。
从$18:00$到次日$6:00$,亮灯时间为$12$小时,每小时耗电量为$0.35kW\cdot h$,则总耗电量为$0.35×12 = 4.2kW\cdot h$。
因为$6>4.2$,所以该太阳能光伏板当日提供的电量能使路灯达到该市政部门规定的亮灯时间。
故答案为:
(1)$y=\frac{2}{5}x + 2(0\leqslant x\leqslant10)$;
(2)能。
(1)设$AB$段$y$与$x$之间的函数表达式为$y = kx + b$。
由图象可知$A(0,2)$,$B(10,6)$($10$小时对应$B$点纵坐标$4 + 2 = 6$),把$A(0,2)$,$B(10,6)$代入$y = kx + b$得:
$\begin{cases}b = 2\\10k + b = 6\end{cases}$
将$b = 2$代入$10k + b = 6$得$10k+2 = 6$,$10k = 4$,解得$k=\frac{2}{5}$。
所以$AB$段$y$与$x$之间的函数表达式为$y=\frac{2}{5}x + 2(0\leqslant x\leqslant10)$。
(2)当$x = 10$时,$y=\frac{2}{5}×10 + 2=6$,即当日发电量为$6kW\cdot h$。
从$18:00$到次日$6:00$,亮灯时间为$12$小时,每小时耗电量为$0.35kW\cdot h$,则总耗电量为$0.35×12 = 4.2kW\cdot h$。
因为$6>4.2$,所以该太阳能光伏板当日提供的电量能使路灯达到该市政部门规定的亮灯时间。
故答案为:
(1)$y=\frac{2}{5}x + 2(0\leqslant x\leqslant10)$;
(2)能。
2. 小连乘地铁上下班,地铁出入口有上、下行自动扶梯和步行楼梯.一段时间后,他发现:乘坐自动扶梯,人距离下层地面平台的高度 $ y $ (单位:$ m $) 与下行时间 $ x $ (单位:$ s $) 之间的一次函数关系如图;走步行楼梯,人距离下层地面平台的高度 $ h $ (单位:$ m $) 与下行时间 $ x $ (单位:$ s $) 的关系如下表.
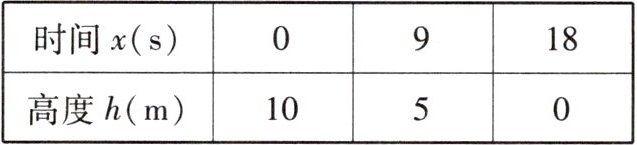
(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 请帮助小连判断,从上层平台到下层地面平台,是乘坐自动扶梯还是走步行楼梯节约时间,并说明理由.
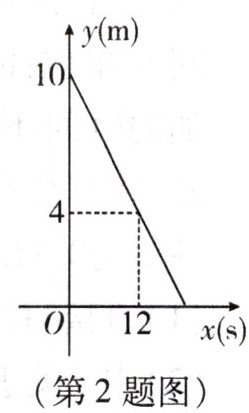

(1) 求 $ y $ 关于 $ x $ 的函数表达式;
(2) 请帮助小连判断,从上层平台到下层地面平台,是乘坐自动扶梯还是走步行楼梯节约时间,并说明理由.

答案:
(1) $ y = -\frac{1}{2}x + 10 $;
(2) 走步行楼梯节约时间,理由见解析。
(1) $ y = -\frac{1}{2}x + 10 $;
(2) 走步行楼梯节约时间,理由见解析。
3. 直线 $ y = ax + b(a \neq 0) $ 过点 $ A(0,1) $,$ B(2,0) $,则关于 $ x $ 的方程 $ ax + b = 0 $ 的解为 (
A.$ x = 0 $
B.$ x = 1 $
C.$ x = 2 $
D.$ x = 3 $
C
)A.$ x = 0 $
B.$ x = 1 $
C.$ x = 2 $
D.$ x = 3 $
答案:
C
4. 若关于 $ x $ 的方程 $ 4ax - b = 0 $ 的解为 $ x = 2 $,则直线 $ y = 4ax - b $ 的图象一定经过点
$(2, 0)$
.
答案:
$(2, 0)$
5. 某生物小组观察一植物生长,得到植物高度 $ y $ (单位:$ cm $) 与观察时间 $ x $ (单位:天) 之间的关系,并画出如图所示的图象 ($ AC $ 是线段,射线 $ CD $ 平行于 $ x $ 轴). 下列说法不正确的是 (
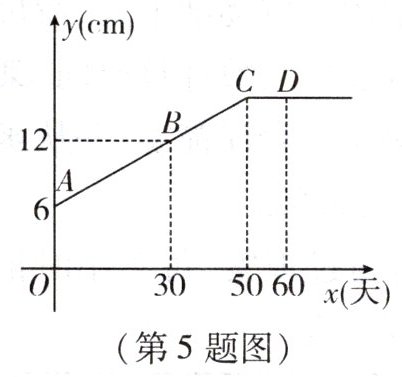
A.从开始观察起,$ 50 $ 天后该植物停止长高
B.直线 $ AC $ 的函数表达式为 $ y = \frac{1}{5}x + 6 $
C.观察第 $ 40 $ 天时,该植物的高度为 $ 14cm $
D.该植物最高为 $ 15cm $
D
)
A.从开始观察起,$ 50 $ 天后该植物停止长高
B.直线 $ AC $ 的函数表达式为 $ y = \frac{1}{5}x + 6 $
C.观察第 $ 40 $ 天时,该植物的高度为 $ 14cm $
D.该植物最高为 $ 15cm $
答案:
D
6. 如图是一次函数 $ y = ax + b $ 的图象,则关于 $ x $ 的方程 $ ax + b = 1 $ 的解为
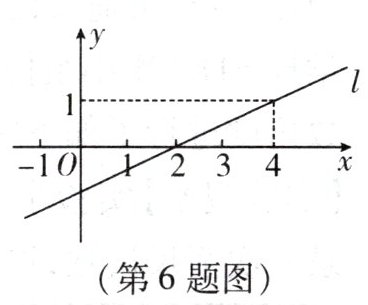
4
.
答案:
$4$
查看更多完整答案,请扫码查看


