第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,在平面直角坐标系中,一动点从原点 $ O $ 出发,沿着箭头所示方向,每次移动 $ 1 $ 个单位长度,依次得到点 $ P_{1}(0,1) $, $ P_{2}(1,1) $, $ P_{3}(1,0) $, $ P_{4}(1,-1) $, $ P_{5}(2,-1) $, $ P_{6}(2,0) $, …$ $,则点 $ P_{2026} $ 的坐标是 (
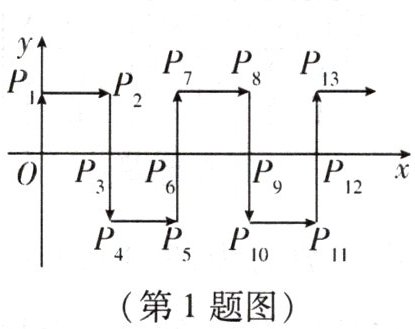
A.$ (675,-1) $
B.$ (675,1) $
C.$ (337,-1) $
D.$ (337,1) $
A
)
A.$ (675,-1) $
B.$ (675,1) $
C.$ (337,-1) $
D.$ (337,1) $
答案:
A
2. 如图,在平面直角坐标系中,$ A(1,1) $, $ B(-1,1) $, $ C(-1,-2) $, $ D(1,-2) $,把一条长为 $ 2024 $ 个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点 $ A $ 处,并按 $ A - B - C - D - A … $ 的规律绕在四边形 $ ABCD $ 的边上,则细线另一端所在位置的点的坐标是 (
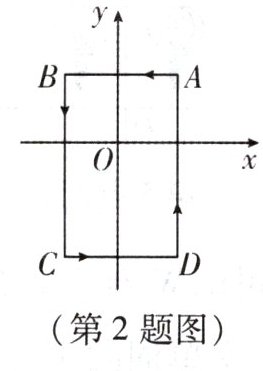
A.$ (-1,-1) $
B.$ (-1,0) $
C.$ (-1,-2) $
D.$ (0,1) $
A
)
A.$ (-1,-1) $
B.$ (-1,0) $
C.$ (-1,-2) $
D.$ (0,1) $
答案:
A
3. 如图,在平面直角坐标系中,将 $ \triangle ABO $ 沿 $ x $ 轴向右滚动到 $ \triangle AB_{1}C_{1} $ 的位置,再到 $ \triangle A_{1}B_{1}C_{2} $ 的位置 ……$ $ 依次进行下去,若已知点 $ A(4,0) $, $ B(0,3) $,则点 $ C_{100} $ 的坐标为 (
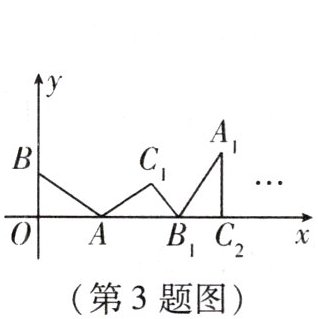
A.$ \left(1200,\dfrac{12}{5}\right) $
B.$ (600,0) $
C.$ \left(600,\dfrac{12}{5}\right) $
D.$ (1200,0) $
B
)
A.$ \left(1200,\dfrac{12}{5}\right) $
B.$ (600,0) $
C.$ \left(600,\dfrac{12}{5}\right) $
D.$ (1200,0) $
答案:
【解析】:
由点A(4,0),B(0,3),O(0,0),得OA=4,OB=3,AB=√(3²+4²)=5,△ABO周长为3+4+5=12,AB边上的高为(3×4)/5=12/5。
滚动规律:△ABO沿x轴向右滚动,每两次滚动(到C₂)横坐标增加一个周长12,且Cₙ纵坐标周期为2(奇数次Cₙ纵坐标为12/5,偶数次为0)。
C₁₀₀为偶数次,横坐标=100/2×12=600,纵坐标=0。
【答案】:B
由点A(4,0),B(0,3),O(0,0),得OA=4,OB=3,AB=√(3²+4²)=5,△ABO周长为3+4+5=12,AB边上的高为(3×4)/5=12/5。
滚动规律:△ABO沿x轴向右滚动,每两次滚动(到C₂)横坐标增加一个周长12,且Cₙ纵坐标周期为2(奇数次Cₙ纵坐标为12/5,偶数次为0)。
C₁₀₀为偶数次,横坐标=100/2×12=600,纵坐标=0。
【答案】:B
4. 如图,正方形 $ ABCD $ 的顶点 $ A(1,1) $, $ B(3,1) $,规定把正方形 $ ABCD $“先沿 $ x $ 轴翻折,再向左平移 $ 1 $ 个单位长度”为一次变换,这样连续经过 $ 2026 $ 次变换后,正方形 $ ABCD $ 的顶点 $ C $ 的坐标为 (

A.$ (-2023,-3) $
B.$ (-2023,3) $
C.$ (-2025,-3) $
D.$ (-2025,3) $
B
)
A.$ (-2023,-3) $
B.$ (-2023,3) $
C.$ (-2025,-3) $
D.$ (-2025,3) $
答案:
B
5. 在平面直角坐标系中,有若干个整数点,其顺序按如图中“$ \to $”方向排列,如 $ (1,0) $; $ (2,0) $, $ (2,1) $; $ (3,2) $, $ (3,1) $, $ (3,0) $; $ (4,0) $, …$ $,根据这个规律探索可得,第 $ 30 $ 个点的坐标为 (
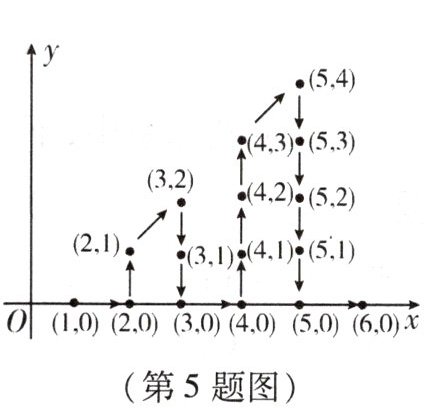
A.$ (8,1) $
B.$ (8,6) $
C.$ (7,1) $
D.$ (7,5) $
A
)
A.$ (8,1) $
B.$ (8,6) $
C.$ (7,1) $
D.$ (7,5) $
答案:
A
6. 在平面直角坐标系中,点 $ A_{1} $ 从原点 $ O $ 出发,沿如图所示的方向运动,到达位置的坐标依次为 $ A_{2}(1,0) $, $ A_{3}(1,1) $, $ A_{4}(-1,1) $, $ A_{5}(-1,-1) $, $ A_{6}(2,-1) $, $ A_{7}(2,2) $, …$ $. 若到达终点 $ A_{n}(506,-505) $,则 $ n $ 的值为
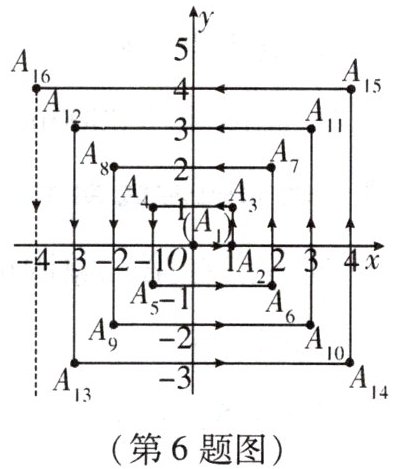
2022
.
答案:
2022
7. 在平面直角坐标系 $ xOy $ 中,对于点 $ P(x,y) $,我们把 $ P_{1}(y - 1,-x - 1) $ 叫作点 $ P $ 的友好点. 已知点 $ A_{1} $ 的友好点为 $ A_{2} $,点 $ A_{2} $ 的友好点为 $ A_{3} $,点 $ A_{3} $ 的友好点为 $ A_{4} $,这样依次得到各点,若 $ A_{1} $ 的坐标为 $ (1,2) $,则 $ A_{2026} $ 的友好点是
(-3,-2)
.
答案:
(-3,-2)
查看更多完整答案,请扫码查看


