《2025年辽宁作业分层培优学案八年级数学上册北师大版》

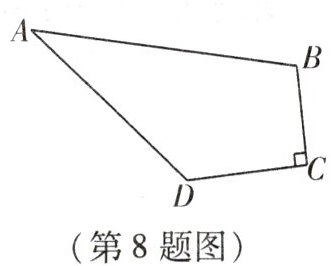
8. 某社区为了让居民享受更多“开窗见景,推门见绿”的空间,决定将一块四边形区域改造为儿童游乐场。如图是该四边形区域的几何示意图,$AB = 25\mathrm{m}$,$BC = 9\mathrm{m}$,$CD = 12\mathrm{m}$,$DA = 20\mathrm{m}$,$\angle C = 90^{\circ}$,按照计划要先在该区域铺设塑胶,已知铺设 $1\mathrm{m}^2$ 塑胶需要 $200$ 元,求铺满该区域需要的费用。

答案： 连接$BD$。
在$\triangle BCD$中，因为$\angle C = 90^{\circ}$，$BC = 9m$，$CD = 12m$，根据勾股定理$BD^{2}=BC^{2}+CD^{2}$，可得：
$BD=\sqrt{9^{2} + 12^{2}}=\sqrt{81 + 144}=\sqrt{225}=15(m)$。
在$\triangle ABD$中，$AB = 25m$，$AD = 20m$，$BD = 15m$，因为$15^{2}+20^{2}=225 + 400 = 625=25^{2}$，满足勾股定理逆定理，所以$\triangle ABD$是直角三角形，$\angle ADB = 90^{\circ}$。
$S_{四边形ABCD}=S_{\triangle ABD}+S_{\triangle BCD}$
$S_{\triangle BCD}=\frac{1}{2}× BC× CD=\frac{1}{2}×9×12 = 54(m^{2})$
$S_{\triangle ABD}=\frac{1}{2}× BD× AD=\frac{1}{2}×15×20 = 150(m^{2})$
则$S_{四边形ABCD}=54 + 150=204(m^{2})$。
已知铺设$1m^{2}$塑胶需要$200$元，则铺满该区域需要的费用为：$204×200 = 40800$（元）。
故铺满该区域需要$40800$元费用。

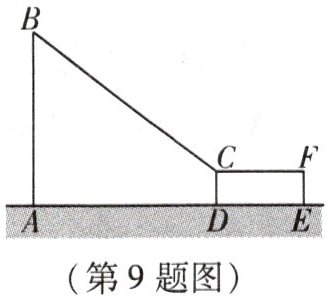
9. 如图是某“飞越丛林”俱乐部打造的一款儿童游戏项目,工作人员告诉小敏,该项目 $AB$ 段和 $BC$ 段均由不锈钢管材打造,总长度为 $26\mathrm{m}$,长方形 $CDEF$ 为一木质平台的截面图。小敏经过现场测量得知 $CD = 1\mathrm{m}$,$AD = 15\mathrm{m}$,于是小敏大胆猜想立柱 $AB$ 段的长为 $10\mathrm{m}$,请判断小敏的猜想是否正确。如果正确,请写出理由；如果不正确,请求出立柱 $AB$ 段的正确长度。

答案： 不正确，AB段的正确长度为9m。

10. 如图,在 $\mathrm{Rt}\triangle ABC$ 中,$\angle C = 90^{\circ}$,把 $\triangle ABC$ 沿直线 $DE$ 折叠,点 $A$ 与点 $B$ 重合。
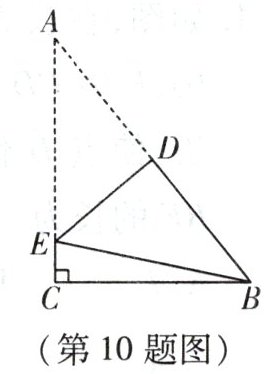
(1)若 $\angle EBC = 16^{\circ}$,求 $\angle A$ 的度数；
(2)若 $AD = 5$,$BC = 6$,求 $CE$ 的长。

答案：
(1)
∵折叠后点A与点B重合，
∴AE=BE，∠EAB=∠EBA。
设∠A=x，则∠EBA=x。
∵∠EBC=16°，
∴∠ABC=∠EBA+∠EBC=x+16°。
在Rt△ABC中，∠A+∠ABC=90°，即x+(x+16°)=90°，
解得2x=74°，x=37°，
∴∠A=37°。
(2)设CE=x，
∵折叠后点A与点B重合，
∴AD=BD=5，AE=BE。
∴AB=AD+BD=10。
在Rt△ABC中，AC²+BC²=AB²，BC=6，
∴AC²=10²-6²=64，AC=8。
则AE=AC-CE=8-x，BE=AE=8-x。
在Rt△BCE中，CE²+BC²=BE²，即x²+6²=(8-x)²，
x²+36=64-16x+x²，
16x=28，x=7/4，
∴CE=7/4。

11. 如图,在一条东西走向的河流的一侧有一村庄 $C$,河边原有两个取水点 $A$,$B$,其中 $AB = AC$,由于某种原因,由 $C$ 到 $A$ 的路现在已经不通,该村为方便村民取水,决定在河边新建一个取水点 $H$($A$,$H$,$B$ 在同一条直线上),并新建一条路 $CH$,测得 $CB = 1.5\mathrm{km}$,$CH = 1.2\mathrm{km}$,$HB = 0.9\mathrm{km}$。
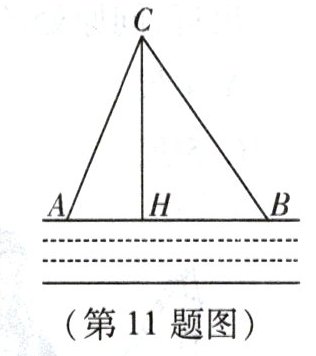
(1)$CH$ 是否为从村庄 $C$ 到河边的最近路？请通过计算加以说明。
(2)新路 $CH$ 比原路 $CA$ 少多少千米？

答案：
(1) 在$\triangle CHB$中，根据勾股定理逆定理：
若$CH^{2}+HB^{2}=CB^{2}$，则$\angle CHB = 90^{\circ}$。
已知$CH = 1.2km$，$HB = 0.9km$，$CB = 1.5km$，
$CH^{2}+HB^{2}=1.2^{2}+0.9^{2}=1.44 + 0.81 = 2.25$，
$CB^{2}=1.5^{2}=2.25$。
因为$CH^{2}+HB^{2}=CB^{2}$，所以$\angle CHB = 90^{\circ}$，即$CH\perp AB$，所以$CH$是从村庄$C$到河边的最近路。
(2) 设$AH=xkm$，因为$AB = AC$，$AB=AH + HB=(x + 0.9)km$，所以$AC=(x + 0.9)km$。
在$Rt\triangle AHC$中，根据勾股定理$AC^{2}=AH^{2}+CH^{2}$，即$(x + 0.9)^{2}=x^{2}+1.2^{2}$。
展开式子得$x^{2}+1.8x + 0.81=x^{2}+1.44$，
移项化简得$1.8x=1.44 - 0.81 = 0.63$，
解得$x = 0.35$。
所以$AC=0.35 + 0.9 = 1.25(km)$。
原路$CA$为$1.25km$，新路$CH$为$1.2km$，
新路$CH$比原路$CA$少$1.25 - 1.2 = 0.05(km)$。
综上，
(1)$CH$是从村庄$C$到河边的最近路；
(2)新路$CH$比原路$CA$少$0.05km$。