第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 某跳远队准备从甲、乙两名运动员中选取一名成绩稳定的参加比赛. 这两名运动员 10 次测试成绩(单位:m)的平均数是$\overline {x}_{甲}= 6.01,\overline {x}_{乙}= 6.01$,方差是$s^{2}_{甲}= 0.01,s^{2}_{乙}= 0.02$,那么应选
甲
去参加比赛.(填“甲”或“乙”)
答案:
甲
2. (新考法·跨生物学科)生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多. 为了解甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率(单位:$\mu mol\cdot m^{-2}\cdot s^{-1}$),结果统计如下:
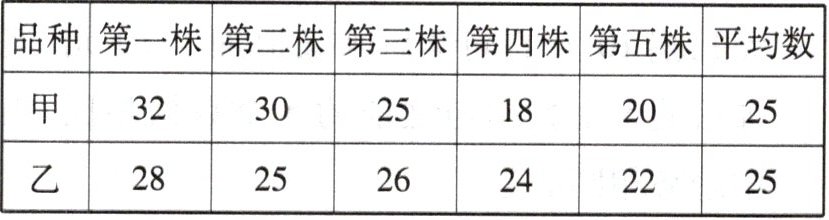
则两个大豆品种中光合作用速率更稳定的是

则两个大豆品种中光合作用速率更稳定的是
乙
.(填“甲”或“乙”)
答案:
乙
3. 8 个砂糖橘的直径(单位:mm)如下:44,43,44,47,44,48,45,42. 按照“组内离差平方和达到最小”的方法,把这 8 个砂糖橘按直径大小分成两组,使每组的“个头”差不多,分组的结果为
(42,43,44,44,44)和(45,47,48)
.
答案:
(42,43,44,44,44)和(45,47,48)
4. 科学家同时培育了甲、乙、丙、丁四种花,下表记录了 4 种花开花时间的平均数和方差,则开花时间最短的并且最平稳的是 (
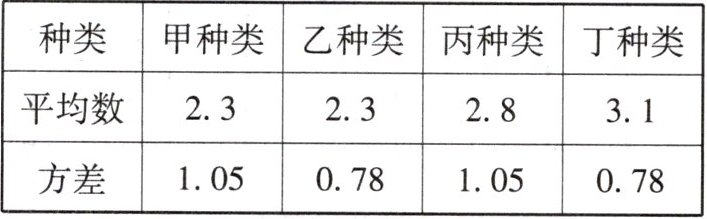
A.甲种类
B.乙种类
C.丙种类
D.丁种类
B
)
A.甲种类
B.乙种类
C.丙种类
D.丁种类
答案:
B
5. 甲、乙、丙、丁四人 10 次随堂测验的成绩如图所示,从图中可以看出这 10 次测验平均成绩较高且较稳定的是 (
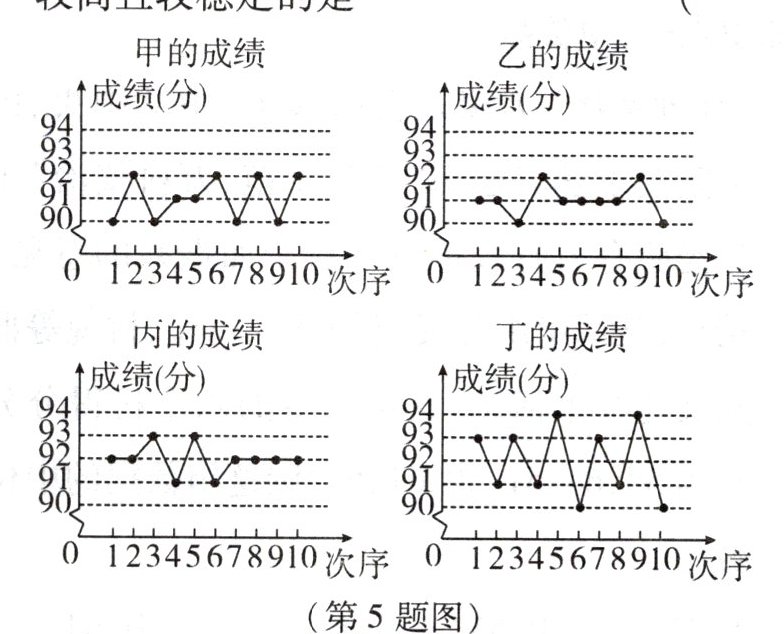
A.甲
B.乙
C.丙
D.丁
C
)
A.甲
B.乙
C.丙
D.丁
答案:
C
6. 要从甲、乙两名同学中选出一名,代表班级参加射击比赛,两人最近 10 次射击训练成绩(单位:环)如下:
甲:7,10,9,5,8,10,8,6,9,8;
乙:8,9,8,8,7,8,9,8,8,7.
(1)甲、乙两人的平均成绩分别是多少?
(2)这两人中,谁的成绩更稳定?
(3)如果其他班级参赛选手的射击成绩都在 7 环左右,本班应该选
甲:7,10,9,5,8,10,8,6,9,8;
乙:8,9,8,8,7,8,9,8,8,7.
(1)甲、乙两人的平均成绩分别是多少?
(2)这两人中,谁的成绩更稳定?
(3)如果其他班级参赛选手的射击成绩都在 7 环左右,本班应该选
乙
参赛更合适;如果其他班级参赛选手的射击成绩都在 9 环左右,本班应该选甲
参赛更合适.
答案:
(1)
$\bar{x}_{甲}=\frac{1}{10}(7 + 10+9 + 5+8 + 10+8 + 6+9 + 8)$
$=\frac{1}{10}×80 = 8$(环)
$\bar{x}_{乙}=\frac{1}{10}(8 + 9+8 + 8+7 + 8+9 + 8+8 + 7)$
$=\frac{1}{10}×80 = 8$(环)
(2)
$s_{甲}^{2}=\frac{1}{10}[(7 - 8)^{2}+(10 - 8)^{2}+(9 - 8)^{2}+(5 - 8)^{2}+(8 - 8)^{2}+(10 - 8)^{2}+(8 - 8)^{2}+(6 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}]$
$=\frac{1}{10}(1 + 4+1 + 9+0+4+0+4+1+0)$
$=\frac{1}{10}×24 = 2.4$
$s_{乙}^{2}=\frac{1}{10}[(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}]$
$=\frac{1}{10}(0 + 1+0+0+1+0+1+0+0+1)$
$=\frac{1}{10}×4 = 0.4$
因为$s_{甲}^{2}>s_{乙}^{2}$,所以乙的成绩更稳定。
(3) 乙;甲
(1)
$\bar{x}_{甲}=\frac{1}{10}(7 + 10+9 + 5+8 + 10+8 + 6+9 + 8)$
$=\frac{1}{10}×80 = 8$(环)
$\bar{x}_{乙}=\frac{1}{10}(8 + 9+8 + 8+7 + 8+9 + 8+8 + 7)$
$=\frac{1}{10}×80 = 8$(环)
(2)
$s_{甲}^{2}=\frac{1}{10}[(7 - 8)^{2}+(10 - 8)^{2}+(9 - 8)^{2}+(5 - 8)^{2}+(8 - 8)^{2}+(10 - 8)^{2}+(8 - 8)^{2}+(6 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}]$
$=\frac{1}{10}(1 + 4+1 + 9+0+4+0+4+1+0)$
$=\frac{1}{10}×24 = 2.4$
$s_{乙}^{2}=\frac{1}{10}[(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}+(8 - 8)^{2}+(9 - 8)^{2}+(8 - 8)^{2}+(8 - 8)^{2}+(7 - 8)^{2}]$
$=\frac{1}{10}(0 + 1+0+0+1+0+1+0+0+1)$
$=\frac{1}{10}×4 = 0.4$
因为$s_{甲}^{2}>s_{乙}^{2}$,所以乙的成绩更稳定。
(3) 乙;甲
查看更多完整答案,请扫码查看


