第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
8. 某出版社出版一种适合中学生阅读的科普读物,当该读物首次出版印刷的印数不少于 $ 5000 $ 册时,投入的成本 $ y $(元)与印数 $ x $(册)之间的相应数据如下表:
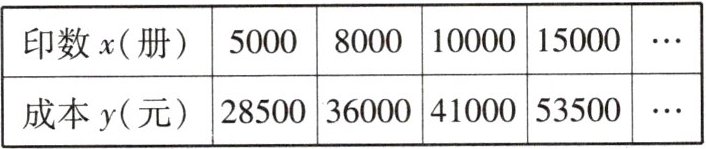
(1) 经过对上表中数据的探究,发现这种读物的投入成本 $ y $(元)是印数 $ x $(册)的一次函数,求这个一次函数的表达式.(不要求写出 $ x $ 的取值范围)
(2) 如果出版社投入成本 $ 48000 $ 元,那么能印该读物多少册?

(1) 经过对上表中数据的探究,发现这种读物的投入成本 $ y $(元)是印数 $ x $(册)的一次函数,求这个一次函数的表达式.(不要求写出 $ x $ 的取值范围)
(2) 如果出版社投入成本 $ 48000 $ 元,那么能印该读物多少册?
答案:
(1)设一次函数表达式为$y=kx+b$,将$x=5000$,$y=28500$和$x=8000$,$y=36000$代入,得$\begin{cases}5000k + b = 28500 \\8000k + b = 36000\end{cases}$,解得$\begin{cases}k = 2.5 \\b = 16000\end{cases}$,表达式为$y = 2.5x+16000$。
(2)当$y = 48000$时,$2.5x+16000=48000$,解得$x = 12800$。
答:
(1)一次函数表达式为$y = 2.5x + 16000$;
(2)能印该读物12800册。
(1)设一次函数表达式为$y=kx+b$,将$x=5000$,$y=28500$和$x=8000$,$y=36000$代入,得$\begin{cases}5000k + b = 28500 \\8000k + b = 36000\end{cases}$,解得$\begin{cases}k = 2.5 \\b = 16000\end{cases}$,表达式为$y = 2.5x+16000$。
(2)当$y = 48000$时,$2.5x+16000=48000$,解得$x = 12800$。
答:
(1)一次函数表达式为$y = 2.5x + 16000$;
(2)能印该读物12800册。
9. 小刚家、学校、图书馆依次在同一条直线上,小刚骑自行车匀速从学校到图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不计). 小刚离家的距离 $ y(\mathrm{m}) $ 与他所用的时间 $ x(\mathrm{min}) $ 的函数关系如图所示.
(1) 小刚家与学校的距离为 $\underline{
(2) 求小刚从图书馆返回家的过程中,$ y $ 与 $ x $ 的函数表达式.
(3) 小刚出发 $ 35 \mathrm{min} $ 时,他离家有多远?

(1) 小刚家与学校的距离为 $\underline{
3000
}\mathrm{m}$,小刚骑自行车的速度为 $\underline{200
}\mathrm{m/min}$.(2) 求小刚从图书馆返回家的过程中,$ y $ 与 $ x $ 的函数表达式.
$y = - 200x + 9000(20\leq x\leq45)$
(3) 小刚出发 $ 35 \mathrm{min} $ 时,他离家有多远?
$2000\mathrm{m}$

答案:
(1) 从图中可知,学校到小刚家距离为$3000 - 0 = 3000$($m$)(当时间为$0$时,离家的距离是$0$,$20min$时离家的距离是$5000m$,此时在图书馆,学校在离家$3000m$处),小刚骑自行车的速度为$(5000 - 3000)÷10 = 200$($m/min$)。
故小刚家与学校的距离为$3000m$,小刚骑自行车的速度为$200m/min$。
(2) 小刚从图书馆返回家所需时间为:
$5000÷200 = 25$($min$)。
$20 + 25 = 45$($min$),即$x$的取值范围是$20\leq x\leq45$。
设$y$与$x$的函数表达式为$y = kx + b$,把$(20,5000)$,$(45,0)$代入得:
$\begin{cases}20k + b = 5000,\\45k + b = 0.\end{cases}$
用$45k + b = 0$减去$20k + b = 5000$可得:
$25k=-5000$,
$k = - 200$,
把$k = - 200$代入$20k + b = 5000$得:
$20×(-200)+b = 5000$,
$-4000 + b = 5000$,
$b = 9000$。
所以$y$与$x$的函数表达式为$y = - 200x + 9000(20\leq x\leq45)$。
(3) 当$x = 35$时,$y=-200×35 + 9000=-7000 + 9000 = 2000$($m$)。
综上,答案依次为:
(1)$3000$,$200$;
(2)$y = - 200x + 9000(20\leq x\leq45)$;
(3)$2000m$。
(1) 从图中可知,学校到小刚家距离为$3000 - 0 = 3000$($m$)(当时间为$0$时,离家的距离是$0$,$20min$时离家的距离是$5000m$,此时在图书馆,学校在离家$3000m$处),小刚骑自行车的速度为$(5000 - 3000)÷10 = 200$($m/min$)。
故小刚家与学校的距离为$3000m$,小刚骑自行车的速度为$200m/min$。
(2) 小刚从图书馆返回家所需时间为:
$5000÷200 = 25$($min$)。
$20 + 25 = 45$($min$),即$x$的取值范围是$20\leq x\leq45$。
设$y$与$x$的函数表达式为$y = kx + b$,把$(20,5000)$,$(45,0)$代入得:
$\begin{cases}20k + b = 5000,\\45k + b = 0.\end{cases}$
用$45k + b = 0$减去$20k + b = 5000$可得:
$25k=-5000$,
$k = - 200$,
把$k = - 200$代入$20k + b = 5000$得:
$20×(-200)+b = 5000$,
$-4000 + b = 5000$,
$b = 9000$。
所以$y$与$x$的函数表达式为$y = - 200x + 9000(20\leq x\leq45)$。
(3) 当$x = 35$时,$y=-200×35 + 9000=-7000 + 9000 = 2000$($m$)。
综上,答案依次为:
(1)$3000$,$200$;
(2)$y = - 200x + 9000(20\leq x\leq45)$;
(3)$2000m$。
10. 已知 $ A $,$ B $ 两地相距 $ 240 \mathrm{km} $,一辆货车从 $ A $ 地前往 $ B $ 地,途中因装载货物停留一段时间. 一辆轿车沿同一条公路从 $ B $ 地前往 $ A $ 地,到达 $ A $ 地后(在 $ A $ 地停留时间不计)立即原路原速返回. 如图是两车距 $ B $ 地的距离 $ y(\mathrm{km}) $ 与货车行驶时间 $ x(\mathrm{h}) $ 之间的函数图象,结合图象回答下列问题:
(1) 图中 $ m $ 的值是 $\underline{
(2) 求货车从 $ A $ 地前往 $ B $ 地的过程中,货车距 $ B $ 地的距离 $ y(\mathrm{km}) $ 与行驶时间 $ x(\mathrm{h}) $ 之间的函数表达式;
(3) 直接写出轿车从 $ B $ 地到 $ A $ 地行驶的过程中,轿车出发多长时间与货车相距 $ 12 \mathrm{km} $.
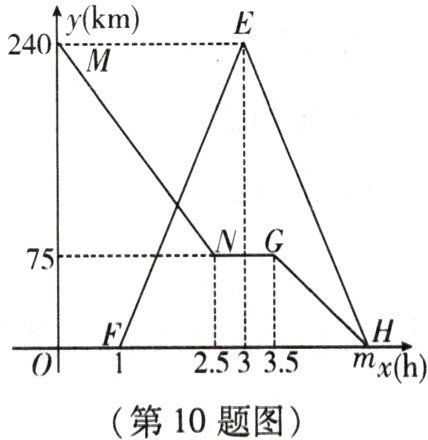
(1) 图中 $ m $ 的值是 $\underline{
4
}$,轿车的速度是 $\underline{160
}\mathrm{km/h}$;(2) 求货车从 $ A $ 地前往 $ B $ 地的过程中,货车距 $ B $ 地的距离 $ y(\mathrm{km}) $ 与行驶时间 $ x(\mathrm{h}) $ 之间的函数表达式;
(3) 直接写出轿车从 $ B $ 地到 $ A $ 地行驶的过程中,轿车出发多长时间与货车相距 $ 12 \mathrm{km} $.

(2) 当 $0 \leq x \leq 2.5$ 时,设 $y = k_1x + b_1$,过点 $(0,240)$ 和 $(2.5,75)$, 代入得 $\begin{cases} b_1 = 240 \\ 2.5k_1 + b_1 = 75 \end{cases}$,解得 $\begin{cases} k_1 = -66 \\ b_1 = 240 \end{cases}$,表达式为 $y = -66x + 240$; 当 $2.5 \leq x \leq 3.5$ 时,停留,$y = 75$; 当 $3.5 \leq x \leq 4$ 时,设 $y = k_2x + b_2$,过点 $(3.5,75)$ 和 $(4,0)$, 代入得 $\begin{cases} 3.5k_2 + b_2 = 75 \\ 4k_2 + b_2 = 0 \end{cases}$,解得 $\begin{cases} k_2 = -150 \\ b_2 = 600 \end{cases}$,表达式为 $y = -150x + 600$。 (3) $\frac{81}{113}$ 小时和 $\frac{93}{113}$ 小时
答案:
(1) 4;160
(2) 当 $0 \leq x \leq 2.5$ 时,设 $y = k_1x + b_1$,过点 $(0,240)$ 和 $(2.5,75)$,
代入得 $\begin{cases} b_1 = 240 \\ 2.5k_1 + b_1 = 75 \end{cases}$,解得 $\begin{cases} k_1 = -66 \\ b_1 = 240 \end{cases}$,表达式为 $y = -66x + 240$;
当 $2.5 \leq x \leq 3.5$ 时,停留,$y = 75$;
当 $3.5 \leq x \leq 4$ 时,设 $y = k_2x + b_2$,过点 $(3.5,75)$ 和 $(4,0)$,
代入得 $\begin{cases} 3.5k_2 + b_2 = 75 \\ 4k_2 + b_2 = 0 \end{cases}$,解得 $\begin{cases} k_2 = -150 \\ b_2 = 600 \end{cases}$,表达式为 $y = -150x + 600$。
(3) $\frac{81}{113}$ 小时和 $\frac{93}{113}$ 小时
(1) 4;160
(2) 当 $0 \leq x \leq 2.5$ 时,设 $y = k_1x + b_1$,过点 $(0,240)$ 和 $(2.5,75)$,
代入得 $\begin{cases} b_1 = 240 \\ 2.5k_1 + b_1 = 75 \end{cases}$,解得 $\begin{cases} k_1 = -66 \\ b_1 = 240 \end{cases}$,表达式为 $y = -66x + 240$;
当 $2.5 \leq x \leq 3.5$ 时,停留,$y = 75$;
当 $3.5 \leq x \leq 4$ 时,设 $y = k_2x + b_2$,过点 $(3.5,75)$ 和 $(4,0)$,
代入得 $\begin{cases} 3.5k_2 + b_2 = 75 \\ 4k_2 + b_2 = 0 \end{cases}$,解得 $\begin{cases} k_2 = -150 \\ b_2 = 600 \end{cases}$,表达式为 $y = -150x + 600$。
(3) $\frac{81}{113}$ 小时和 $\frac{93}{113}$ 小时
查看更多完整答案,请扫码查看


