《2025年辽宁作业分层培优学案八年级数学上册北师大版》

9. 下列说法中,错误的是(B)
A.无理数的相反数还是无理数
B.有理数就是有限小数
C.正实数包括正有理数和正无理数
D.无论有理数还是无理数都是实数

答案： B

10. 写出一个大于 -4 的负无理数:$-\sqrt{2}$（答案不唯一）.

答案： $-\sqrt{2}$（答案不唯一）

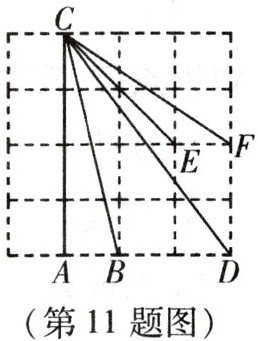
11. 如图是由 16 个边长为 1 的小正方形拼成的大正方形,连接$CA,CB,CD,CE,CF$五条线段,其中长度是无理数的有3条.

答案： 3

12. 直角三角形两直角边长为 2 和 3,斜边在两个相邻的整数之间,这两个整数是3和4.

答案： 3，4

13. 聪聪在学完实数后,对数进行分类时,发现“实数”“整数”“正数”“无理数”有如图所示的关系,请你在图中的横线上按对应序号分别填上一个适合的数.

答案： ①-1/2；②1/2；③2；④√2；⑤-3；⑥-√2

14. 已知面积为 7 的正方形的边长为$x$,请你回答下列问题.
(1)$x$的整数部分是多少?
(2)把$x$的值精确到十分位是多少? 精确到百分位呢?
(3)$x$是有理数吗? 请简要说明理由.

答案：
(1)
因为正方形面积为$7$，根据正方形面积公式$S = x^{2}$（$S$为面积，$x$为边长），可得$x^{2}=7$，$x=\sqrt{7}$（$x\gt0$）。
由于$4\lt7\lt9$，那么$\sqrt{4}\lt\sqrt{7}\lt\sqrt{9}$，即$2\lt x\lt3$，所以$x$的整数部分是$2$。
(2)
因为$2.6^{2}=6.76$，$2.7^{2} = 7.29$，且$6.76\lt7\lt7.29$，所以$2.6\lt x\lt2.7$，精确到十分位是$2.6$（这里采用夹值法，更接近$2.6$？实际$2.64^{2}=6.9696$，$2.65^{2}=7.0225$，所以精确到十分位$x\approx2.6$说法错误，应精确到十分位是$2.6$（按四舍五入$x\approx 2.6$（十分位后一位$4\lt5$舍去），精确说法：
因为$2.64^{2}=6.9696\lt7$，$2.65^{2}=7.0225\gt7$，所以精确到十分位$x\approx2.6$（根据四舍五入，十分位后是$4$舍去）；
精确到百分位，因为$2.64^{2}=6.9696\lt7$，$2.65^{2}=7.0225\gt7$，更接近$2.645$，$2.645^{2}=6.996025\lt7$，$2.646^{2}=7.001316\gt7$，所以精确到百分位$x\approx2.65$。
(3)
$x$不是有理数。
因为假设$x$是有理数，那么$x$可以表示为两个整数之比$\frac{p}{q}$（$p$、$q$为互质的整数，$q\neq0$），则$x^{2}=\frac{p^{2}}{q^{2}} = 7$，即$p^{2}=7q^{2}$，所以$p^{2}$是$7$的倍数，那么$p$也是$7$的倍数，设$p = 7m$（$m$为整数），则$(7m)^{2}=7q^{2}$，$49m^{2}=7q^{2}$，$q^{2}=7m^{2}$，所以$q$也是$7$的倍数，这与$p$、$q$互质矛盾，所以$x$不是有理数。
综上，答案依次为：
(1)$2$；
(2)精确到十分位是$2.6$，精确到百分位是$2.65$；
(3)$x$不是有理数，理由如上述。

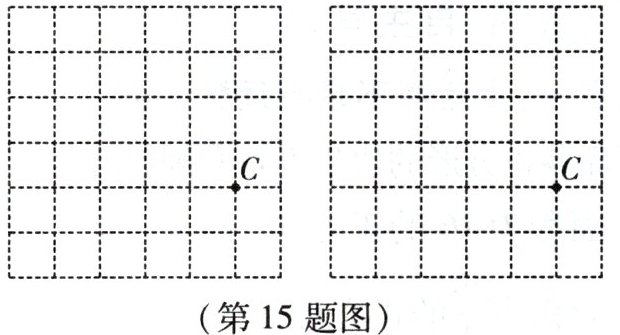
15. 如图,在正方形网格中,每个小正方形的边长均为 1. 已知点$C$,请你按要求设计$\triangle ABC$,使$∠C = 90^{\circ},AC = BC$.
(1)$AB$的长为无理数,$AC,BC$的长均为有理数;
(2)三边的长均为无理数.

答案：
(1) 设点C为网格中一点，取点A在点C右侧3个单位长度处，点B在点C上方3个单位长度处。则AC=3，BC=3（均为有理数），AB=√(3²+3²)=3√2（无理数）。
(2) 取点A在点C向右1个单位长度且向上2个单位长度处，点B在点C向右2个单位长度且向下1个单位长度处。则AC=√(1²+2²)=√5，BC=√(2²+(-1)²)=√5，AB=√((1-2)²+(2+1)²)=√10（均为无理数）。

16. 数学课上,好学的小明向老师提出了一个问题:无限循环小数是无理数吗?
以$0.\dot{3}$为例,老师给小明做了以下解答:
设$0.\dot{3}为x$,即$0.33… = x$.
等式两边同时乘 10,得$3.33… = 10x$,即$3 + 0.\dot{3} = 10x$.
因为$0.\dot{3} = x$,所以$3 + x = 10x$,解得$x = \frac{1}{3}$,即$0.\dot{3} = \frac{1}{3}$.
因为分数是有理数,所以$0.\dot{3}$是有理数.
请根据上述阅读,解决下列问题:
(1) 无限循环小数$0.\dot{2}$写成分数的形式是$\frac{2}{9}$;
(2) 请用解方程的办法将$0.\dot{2}\dot{1}$写成分数.

答案：
(1) 设 $0.\dot{2} = x$，
等式两边同时乘 10，得 $2.22\ldots = 10x$，
即 $2 + 0.\dot{2} = 10x$，
因为 $0.\dot{2} = x$，
所以 $2 + x = 10x$，
解得 $x = \frac{2}{9}$，
即 $0.\dot{2} = \frac{2}{9}$。
答案为：$\frac{2}{9}$。
(2) 设 $0.\dot{2}\dot{1} = x$，
等式两边同时乘 100，得 $21.2121\ldots = 100x$，
即 $21 + 0.\dot{2}\dot{1} = 100x$，
因为 $0.\dot{2}\dot{1} = x$，
所以 $21 + x = 100x$，
解得 $x = \frac{21}{99} = \frac{7}{33}$，
即 $0.\dot{2}\dot{1} = \frac{7}{33}$。