《2025年辽宁作业分层培优学案八年级数学上册北师大版》

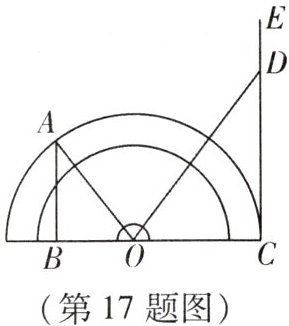
17. (7 分)(新考法·跨物理学科)小丽在物理实验课上利用如图所示“光的反射演示器”直观呈现了光的反射原理. 她用激光笔从量角器左边边缘点 $ A $ 处发出光线,经量角器圆心 $ O $ 处(此处放置平面镜)反射后,反射光线落在右边光屏 $ CE $ 上的点 $ D $ 处($ C $ 也在量角器的边缘上,$ O $ 为量角器的中心,$ C $,$ O $,$ B $ 三点共线,$ AB \perp BC $,$ CE \perp BC $). 小丽在实验中还记录下了 $ AB = 6 $cm,$ BC = 12 $cm. 依据记录的数据,求量角器的半径 $ OC $ 长.

答案： 解：设量角器半径 $ OC = r $，因为 $ C、O、B $ 三点共线且 $ BC = 12\ cm $，设 $ BO = x $，则 $ OC = 12 - x $，故 $ r = 12 - x $。
由于 $ A $ 是量角器边缘点，$ O $ 为中心，所以 $ OA = OC = r $。在 $ Rt\triangle ABO $ 中，$ AB \perp BC $，$ AB = 6\ cm $，由勾股定理得：
$ OA^2 = AB^2 + BO^2 $，即 $ r^2 = 6^2 + x^2 $。
根据光的反射定律，入射角等于反射角，结合 $ AB \perp BC $、$ CE \perp BC $，可得 $ \tan(入射角) = \tan(反射角) $，即 $ \frac{BO}{AB} = \frac{OC}{CE} $（此处利用几何关系推导得 $ \frac{x}{6} = \frac{12 - x}{y} $，但核心等式为 $ OA = OC $）。
将 $ r = 12 - x $ 代入勾股定理式子：
$ (12 - x)^2 = 6^2 + x^2 $
展开得：$ 144 - 24x + x^2 = 36 + x^2 $
化简：$ 24x = 108 $
解得 $ x = 4.5 $。
则 $ OC = r = 12 - x = 12 - 4.5 = 7.5\ cm $。
答：量角器的半径 $ OC $ 长为 $ 7.5\ cm $。

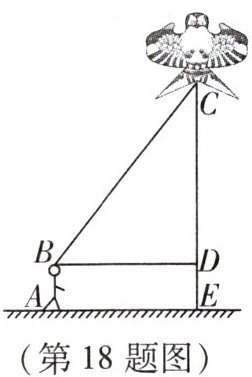
18. (10 分)“儿童散学归来早,忙趁东风放纸鸢.”又到了放风筝的最佳时节,小明和小亮学习了“勾股定理”之后,为了测得风筝的垂直高度 $ CE $(如图),他们进行了如下操作：
①测得水平距离 $ BD $ 的长为 15m；②根据手中剩余线的长度计算出风筝线 $ BC $ 的长为 25m；③牵线放风筝的小明的身高为 1.6m.
(1) 求风筝的垂直高度 $ CE $；
(2) 如果小明想风筝沿 $ CD $ 方向下降 12m,那么他应该往回收线多少米？

答案：
(1) 由题意知，四边形ABDE是矩形，所以$BD=AE=15m$，$AB=DE=1.6m$，$\angle CDB=90°$。
在$Rt\triangle CBD$中，$BC=25m$，$BD=15m$，根据勾股定理$CD^2 + BD^2 = BC^2$，得：
$CD^2 = BC^2 - BD^2 = 25^2 - 15^2 = 625 - 225 = 400$，所以$CD = 20m$。
则$CE = CD + DE = 20 + 1.6 = 21.6m$。
(2) 风筝沿$CD$方向下降12m后，新位置为点$C'$，则$CC' = 12m$，所以$C'D = CD - CC' = 20 - 12 = 8m$。
在$Rt\triangle C'BD$中，$BD=15m$，$C'D=8m$，根据勾股定理$BC'^2 = C'D^2 + BD^2 = 8^2 + 15^2 = 64 + 225 = 289$，所以$BC' = 17m$。
往回收线的长度为$BC - BC' = 25 - 17 = 8m$。
(1) 21.6m；
(2) 8m。

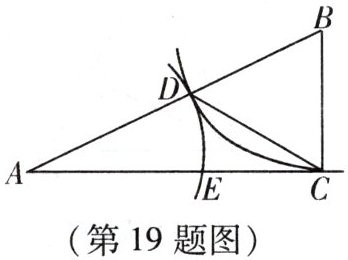
19. (10 分)如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,以点 $ B $ 为圆心,$ BC $ 长为半径画弧,交线段 $ AB $ 于点 $ D $,以点 $ A $ 为圆心,$ AD $ 长为半径画弧,交线段 $ AC $ 于点 $ E $.
(1) 若 $ \angle A = 26^{\circ} $,求 $ \angle ACD $ 的度数；
(2) 若 $ BC = 8 $,$ CE = 6 $,求 $ AD $ 的长.

答案：
(1)$32^{\circ}$；
(2)$9$。