《2025年辽宁作业分层培优学案八年级数学上册北师大版》

1. 盲盒顾名思义就是盒子中放置不同的物品,消费者凭运气抽中商品,正是这种随机化的体验,让消费者产生消费欲望,成为当下最热门的营销方法之一. 某葡萄酒酒庄为回馈新老客户,也推出了盲盒式营销. 酒庄计划在每件盲盒中放人 A,B 两种类型的酒. 销售人员先包装了甲、乙两种盲盒. 甲盲盒中装了 A 种酒 4 瓶,B 种酒 4 瓶;乙盲盒中装了 A 种酒 2 瓶,B 种酒 5 瓶;经过测算,甲盲盒的成本价为每件 280 元,乙盲盒的成本价为每件 200 元. 请计算 A 种酒和 B 种酒的成本价分别为每瓶多少元.

答案： 设 A 种酒的成本价为每瓶 $x$ 元，B 种酒的成本价为每瓶 $y$ 元。
根据题意，列出以下方程组：
$\begin{cases}4x + 4y = 280, \\2x + 5y = 200.\end{cases}$
将第一个方程乘以$\frac{1}{4}$，第二个方程乘以$\frac{1}{1}$，得到：
$\begin{cases}x + y = 70, \\2x + 5y = 200.\end{cases}$
用$x + y = 70$乘以2得到：
$2x+2y=140$，
用$2x + 5y = 200$减去$2x+2y=140$，得到：
$3y=60$，
解得$y=20$，
将$y=20$带入$x + y = 70$，得到：
$x+20=70$，
解得$x = 50$，
所以方程组的解为：
$\begin{cases} x = 50, \\ y = 20. \end{cases}$
答：A 种酒的成本价为每瓶 50 元，B 种酒的成本价为每瓶 20 元。

2. 分别用 8 个大小一样的小长方形拼图. 如图 1,小明拼成了一个大的长方形;如图 2,小红拼成了一个大的正方形,但中间恰好空出一个边长为 1cm 的小正方形. 你能求出小长方形的长和宽吗?

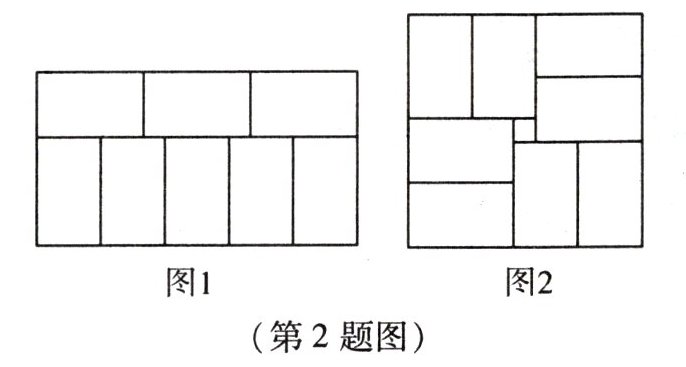
(第 2 题图)

答案： 设小长方形的长为$x\,cm$，宽为$y\,cm$。
由图1可得方程：
大长方形的长由3个小长方形的长组成，同时也由5个小长方形的宽组成，因此$3x = 5y$。
由图2可得方程：
大正方形边长可表示为小长方形的长与2个宽的和，同时中间空出边长1cm的小正方形，结合小长方形长宽关系可得$x = 2y - 1$。
解方程组：
$\begin{cases}3x = 5y \\x = 2y - 1\end{cases}$
将$x = 2y - 1$代入$3x = 5y$：
$3(2y - 1) = 5y$
$6y - 3 = 5y$
$y = 3$
将$y = 3$代入$x = 2y - 1$：
$x = 2×3 - 1 = 5$
结论：
小长方形的长为$5\,cm$，宽为$3\,cm$。
$\boxed{长为5\,cm，宽为3\,cm}$

3. 甲、乙两城相距 1120km,一列快车从甲城出发 120km 后,另一列动车从乙城出发开往甲城,2h 后两车相遇. 若快车平均每小时行驶的路程比动车平均每小时行驶的路程的一半多 5km,则动车与快车平均每小时各行驶多少千米?

答案： 设动车平均每小时行驶 $x$ 千米，快车平均每小时行驶 $y$ 千米。
根据题意，可以列出以下方程组：
$\begin{cases}y = \frac{1}{2}x + 5, \\1120 - 120 = 2(x + y).\end{cases}$
将第一个方程代入第二个方程，得：
$1000 = 2(x + \frac{1}{2}x + 5)$，
$1000 = 2(\frac{3}{2}x + 5)$，
$1000 = 3x + 10$，
$3x = 990$，
$x = 330$。
将 $x = 330$ 代入第一个方程，得：
$y = \frac{1}{2} × 330 + 5$，
$y = 165 + 5$，
$y = 170$。
答：动车平均每小时行驶 $330$ 千米，快车平均每小时行驶 $170$ 千米。

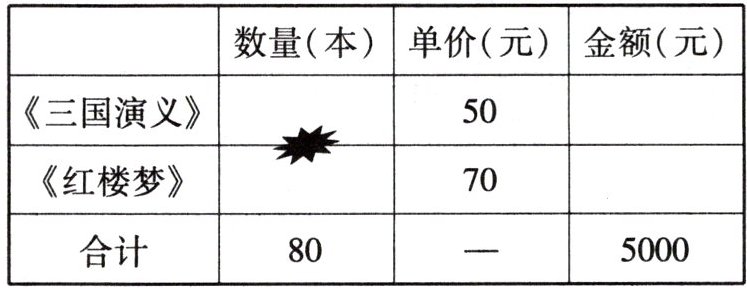
4. (新考法·创设真实情境)为传承优秀传统文化,某中学计划为校图书馆购人一批文学名著,恰逢书店在做促销活动,采购员王老师在该书店购买了《三国演义》和《红楼梦》若干本.
(1)回到学校后王老师发现购物单被弄花了,如下表所示. 请根据购物单中的数据求出《三国演义》和《红楼梦》各购买了多少本.
(2)将新购买的《三国演义》和《红楼梦》放置在两个书架上,若 A 书架上放置的数量比 B 书架上放置的 2 倍多 5 本,两个书架上各放置图书多少本?

（1）设《三国演义》购买了$x$本，《红楼梦》购买了$y$本。
$\begin{cases}x + y = 80,\\50x + 70y = 5000.\end{cases}$
由$x + y = 80$得$x = 80 - y$，
将$x = 80 - y$代入$50x + 70y = 5000$中：
$50×(80 - y) + 70y = 5000$，
$4000 - 50y + 70y = 5000$，
$20y = 1000$，
$y = 50$。
将$y = 50$代入$x = 80 - y$得$x = 30$。
所以方程组的解为$\begin{cases}x = 30,\\y = 50.\end{cases}$
答：《三国演义》购买了$30$本，《红楼梦》购买了$50$本。
（2）由（1）可知总共有$30 + 50 = 80$本书。
设$B$书架上放置$m$本，则$A$书架上放置$(2m + 5)$本。
$m + 2m + 5 = 80$，
$3m = 75$，
$m = 25$。
$2m + 5 = 2×25 + 5 = 55$。
答：$A$书架上放置$55$本，$B$书架上放置$25$本。

答案： （1）设《三国演义》购买了$x$本，《红楼梦》购买了$y$本。
$\begin{cases}x + y = 80,\\50x + 70y = 5000.\end{cases}$
由$x + y = 80$得$x = 80 - y$，
将$x = 80 - y$代入$50x + 70y = 5000$中：
$50×(80 - y) + 70y = 5000$，
$4000 - 50y + 70y = 5000$，
$20y = 1000$，
$y = 50$。
将$y = 50$代入$x = 80 - y$得$x = 30$。
所以方程组的解为$\begin{cases}x = 30,\\y = 50.\end{cases}$
答：《三国演义》购买了$30$本，《红楼梦》购买了$50$本。
（2）由（1）可知总共有$30 + 50 = 80$本书。
设$B$书架上放置$m$本，则$A$书架上放置$(2m + 5)$本。
$m + 2m + 5 = 80$，
$3m = 75$，
$m = 25$。
$2m + 5 = 2×25 + 5 = 55$。
答：$A$书架上放置$55$本，$B$书架上放置$25$本。