《2025年辽宁作业分层培优学案八年级数学上册北师大版》

17. (8 分)已知 y 与 $x + 1$ 成正比例,当 $x = 2$ 时,$y = 9$.
(1)求 y 与 x 之间的函数表达式.
(2)当 x 取多少时,$y = -9$？

答案：
(1)$y = 3x+3$；
(2)$x = - 4$。

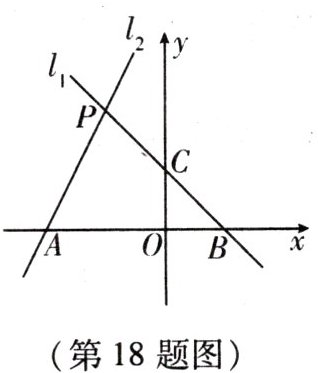
18. (8 分)如图,已知过点$C(0, 1)的直线l_1与直线l_2: y = 2x + 4相交于点P(-1, a)$.
(1)求直线$l_1$的函数表达式；
(2)求四边形 PAOC 的面积.

答案：
(1) 因为点P(-1,a)在直线l₂:y=2x+4上，将x=-1代入得a=2×(-1)+4=2，所以P(-1,2)。设直线l₁的表达式为y=kx+b，
∵l₁过点C(0,1)和P(-1,2)，
∴b=1，将P(-1,2)代入得2=-k+1，解得k=-1，
∴直线l₁的表达式为y=-x+1。
(2) 对于直线l₂:y=2x+4，令y=0得x=-2，
∴A(-2,0)。四边形PAOC的顶点坐标为P(-1,2)、A(-2,0)、O(0,0)、C(0,1)。由坐标得S四边形PAOC=S△PAO+S△PCO。S△PAO=1/2×AO×|yP|=1/2×2×2=2；S△PCO=1/2×OC×|xP|=1/2×1×1=1/2。
∴S四边形PAOC=2+1/2=5/2。
(1) y=-x+1；
(2) 5/2

19. (8 分)某新能源汽车企业对一款新能源汽车进行性能测试. 测试前该新能源汽车已充满电,测试时汽车保持匀速运动,相关测试数据如下表.

这辆新能源汽车电池的剩余电量 y(单位：$kW·h$)与行驶时间 x(单位：h),行驶路程 s(单位：km)与行驶时间 x(单位：h)之间满足不同的一次函数关系.
(1)①直接写出 s 与 x 之间的函数关系式：$s = 80x$；
②求 y 与 x 之间的函数关系式.(以上两问均不要求写出自变量 x 的取值范围)
(2)当这款新能源汽车剩余电量为总电量的 10% 时,必须停止测试开始充电,否则将对汽车造成严重损伤. 求这辆车从开始测试到再次充电时行驶的最远路程.

答案：
(1)① $s = 80x$；
②设$y = kx + b$，把$(0,80)$，$(1,65)$代入得：
$\begin{cases}b = 80\\k + b = 65\end{cases}$
解得$\begin{cases}k = - 15\\b = 80\end{cases}$
所以$y$与$x$之间的函数关系式为$y = - 15x + 80$；
(2)当$y = 80×10\% = 8$时，$-15x + 80 = 8$，
$-15x = - 72$，
$x = 4.8$，
把$x = 4.8$代入$s = 80x$，得$s = 80×4.8 = 384(km)$。
答：这辆车从开始测试到再次充电时行驶的最远路程为$384km$。