第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
7. 李师傅将容量为 $ 60L $ 的货车油箱加满后,从工厂出发运送一批物资到某地.行驶过程中,货车离目的地的路程 $ s $ (单位:$ km $) 与行驶时间 $ t $ (单位:$ h $) 的关系如图所示 (中途休息、加油的时间不计). 当油箱中剩余油量为 $ 10L $ 时,货车会自动显示加油提醒.若货车平均耗油量为 $ 0.1L/km $,请根据图象解答下列问题:
(1) 直接写出工厂离目的地的路程;
(2) 求 $ s $ 关于 $ t $ 的函数表达式;
(3) 当货车显示加油提醒后,问行驶时间 $ t $ 在怎样的范围内货车应进站加油.

(1) 直接写出工厂离目的地的路程;
(2) 求 $ s $ 关于 $ t $ 的函数表达式;
(3) 当货车显示加油提醒后,问行驶时间 $ t $ 在怎样的范围内货车应进站加油.

答案:
(1)880;(2)s=-80t+880;(3)6.25≤t<7.5。
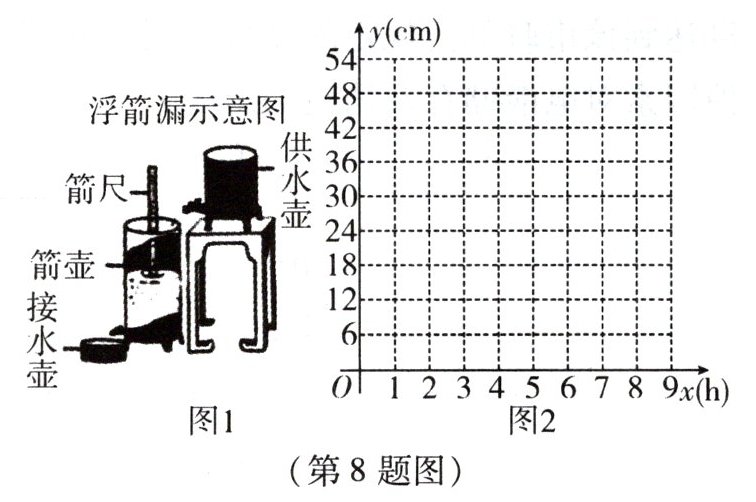
8. (新考法·数学文化)《九章算术》中记载,浮箭漏 (图 1) 出现于汉武帝时期,它由供水壶和箭壶组成,箭壶内装有箭尺,水匀速地从供水壶流到箭壶,箭壶中的水位逐渐上升,箭尺匀速上浮,可通过读取箭尺读数计算时间.某学校 STEAM 小组仿制了一套浮箭漏,并从函数角度进行了如下实验探究:
【实验观察】
实验小组通过观察,每 $ 2 $ 小时记录一次箭尺读数,得到下表.
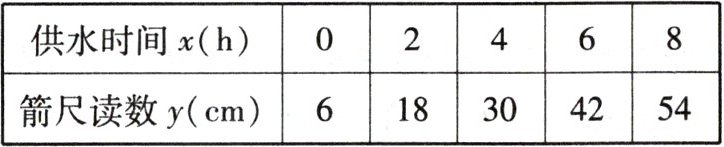
【探索发现】
(1) 建立平面直角坐标系,如图 $ 2 $,横轴表示供水时间 $ x $,纵轴表示箭尺读数 $ y $,描出以表格中数据为坐标的各点.
(2) 观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由.
【结论应用】
应用上述发现的规律估算:
(1) 供水时间达到 $ 12h $ 时,箭尺的读数为多少厘米?
(2) 如果本次实验记录的开始时间是上午 $ 8:00 $,那么当箭尺读数为 $ 90cm $ 时是几点钟? (箭尺最大读数为 $ 100cm $)
浮箭漏示意图
【实验观察】
实验小组通过观察,每 $ 2 $ 小时记录一次箭尺读数,得到下表.

【探索发现】
(1) 建立平面直角坐标系,如图 $ 2 $,横轴表示供水时间 $ x $,纵轴表示箭尺读数 $ y $,描出以表格中数据为坐标的各点.
(2) 观察上述各点的分布规律,判断它们是否在同一条直线上,如果在同一条直线上,求出这条直线所对应的函数表达式;如果不在同一条直线上,说明理由.
【结论应用】
应用上述发现的规律估算:
(1) 供水时间达到 $ 12h $ 时,箭尺的读数为多少厘米?
(2) 如果本次实验记录的开始时间是上午 $ 8:00 $,那么当箭尺读数为 $ 90cm $ 时是几点钟? (箭尺最大读数为 $ 100cm $)
浮箭漏示意图

答案:
【探索发现】
(2) 在同一条直线上.
设函数表达式为 $y = kx + b$,
把 $x = 0, y = 6$ 和 $x = 2, y = 18$ 代入得:
$\begin{cases}b = 6, \\2k + b = 18,\end{cases}$
解得$\begin{cases}k = 6, \\b = 6.\end{cases}$
所以函数表达式为 $y = 6x + 6$,
当 $x = 4$ 时,$y = 6× 4 + 6 = 30$;
当 $x = 6$ 时,$y = 6× 6 + 6 = 42$;
当 $x = 8$ 时,$y = 6× 8 + 6 = 54$,
与表格中数据一致,所以各点在同一条直线上,函数表达式为 $y = 6x + 6$。
【结论应用】
(1) 当 $x = 12$ 时,$y = 6× 12 + 6 = 78$,
所以供水时间达到 $12h$ 时,箭尺的读数为 $78$ 厘米。
(2) 当 $y = 90$ 时,$90 = 6x + 6$,
解得$x = 14$,
因为实验记录开始时间是上午 $8:00$,经过 $14$ 小时后是 $22:00$(即晚上 $10$ 点)。
综上,答案为:当箭尺读数为 $90cm$ 时是 $22:00$。
(2) 在同一条直线上.
设函数表达式为 $y = kx + b$,
把 $x = 0, y = 6$ 和 $x = 2, y = 18$ 代入得:
$\begin{cases}b = 6, \\2k + b = 18,\end{cases}$
解得$\begin{cases}k = 6, \\b = 6.\end{cases}$
所以函数表达式为 $y = 6x + 6$,
当 $x = 4$ 时,$y = 6× 4 + 6 = 30$;
当 $x = 6$ 时,$y = 6× 6 + 6 = 42$;
当 $x = 8$ 时,$y = 6× 8 + 6 = 54$,
与表格中数据一致,所以各点在同一条直线上,函数表达式为 $y = 6x + 6$。
【结论应用】
(1) 当 $x = 12$ 时,$y = 6× 12 + 6 = 78$,
所以供水时间达到 $12h$ 时,箭尺的读数为 $78$ 厘米。
(2) 当 $y = 90$ 时,$90 = 6x + 6$,
解得$x = 14$,
因为实验记录开始时间是上午 $8:00$,经过 $14$ 小时后是 $22:00$(即晚上 $10$ 点)。
综上,答案为:当箭尺读数为 $90cm$ 时是 $22:00$。
查看更多完整答案,请扫码查看


