《2025年辽宁作业分层培优学案八年级数学上册北师大版》

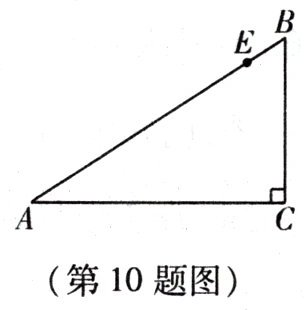
10. 如图,在$\triangle ABC$中,已知$∠ACB= 90^{\circ},AC= $12,$BC= 9$.
(1)求 AB 的长;
(2)D 为 CB 上的一点,将$\triangle ACD$沿直线 AD 翻折,点 C 恰好落在 AB 边上的点 E 处,请利用无刻度的直尺和圆规作出点 D(不写作法,保留作图痕迹),并求出 CD 的长.

答案：
(1) 在Rt△ABC中，∠ACB=90°，AC=12，BC=9，由勾股定理得：
AB²=AC²+BC²=12²+9²=144+81=225，
∴AB=15。
(2) 作图痕迹：①以A为圆心，AC长为半径画弧交AB于点E；②连接CE；③作CE的垂直平分线交CB于点D。
设CD=x，由折叠性质得AE=AC=12，DE=CD=x，∠AED=∠C=90°，
∴BE=AB-AE=15-12=3，∠DEB=90°。
在Rt△DEB中，DE²+BE²=DB²，即x²+3²=(9-x)²，
解得x=4，
∴CD=4。

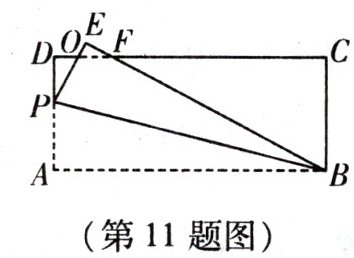
11. 如图,在长方形 ABCD 中,$AB= 12,BC= 5,$点 P 为 AD 上一点,将$\triangle ABP$沿 BP 翻折至$\triangle EBP$,PE 与 CD 相交于点 O,BE 与 CD 相交于点 F,且$OP= OF$.
(1)试说明:$OE= OD$;
(2)求 AP 的长.

答案：
(1) 见解析；
(2) 60/19。

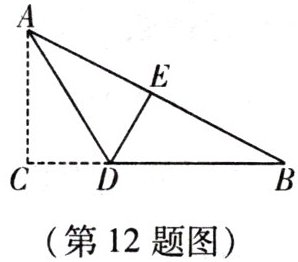
12. 如图,三角形纸片 ABC 的三边长分别为$AC= $6,$BC= 8$,$AB= 10$,现将边 AC 沿 AD 折叠,使它落在边 AB 上,点 C 与点 E 重合. 求 CD 的长.

答案：
∵AC=6，BC=8，AB=10，
∴AC²+BC²=6²+8²=36+64=100=10²=AB²，
∴△ABC是直角三角形，∠C=90°．
由折叠性质得：AE=AC=6，DE=CD，∠AED=∠C=90°，
∴∠DEB=180°-∠AED=90°，EB=AB-AE=10-6=4．
设CD=x，则DE=x，DB=BC-CD=8-x．
在Rt△DEB中，由勾股定理得：DE²+EB²=DB²，
即x²+4²=(8-x)²，
x²+16=64-16x+x²，
16x=48，
x=3．
∴CD的长为3．

13. (沈阳期中)正方形 ABCD 的边长是 9,点 E在边 AB 上,$AE= 4$,点 F 在直线 BC 上(点 F不与点 B 重合). 将$\triangle EBF$沿 EF 折叠,点 B落在点$B'$处,当$∠CDB'= 90^{\circ}$时,求 CF 的长.

答案： 解：
建立平面直角坐标系，设正方形 $ABCD$ 中 $A(0,0)$，$B(9,0)$，$C(9,9)$，$D(0,9)$。
点 $E$ 在 $AB$ 上，$AE=4$，则 $E(4,0)$，$EB=AB-AE=5$。
设 $F$ 在直线 $BC$ 上，坐标为 $(9,t)$（$t \neq 0$），折叠后 $B$ 落在 $B'$ 处，由折叠性质得 $EB'=EB=5$，$FB'=FB=|t|$。
关键条件：$\angle CDB'=90°$
$D(0,9)$，$C(9,9)$，向量 $\overrightarrow{DC}=(9,0)$。设 $B'(x,y)$，则 $\overrightarrow{DB'}=(x,y-9)$。
由 $\angle CDB'=90°$，得 $\overrightarrow{DC} \cdot \overrightarrow{DB'}=0$，即 $9x=0$，故 $x=0$，$B'(0,y)$。
由 $EB'=5$ 求 $B'$ 坐标
$E(4,0)$，$B'(0,y)$，则 $\sqrt{(4-0)^2+(0-y)^2}=5$，解得 $y^2=9$，$y=3$ 或 $y=-3$。
分情况求 $CF$
情况1：$B'(0,3)$
$FB'=FB$，$F(9,t)$，则 $\sqrt{(9-0)^2+(t-3)^2}=|t|$。
平方得 $81+(t-3)^2=t^2$，解得 $t=15$。
$F(9,15)$，$CF=|15-9|=6$。
情况2：$B'(0,-3)$
$FB'=FB$，则 $\sqrt{(9-0)^2+(t+3)^2}=|t|$。
平方得 $81+(t+3)^2=t^2$，解得 $t=-15$。
$F(9,-15)$，$CF=| -15-9|=24$。
结论：$CF$ 的长为 $6$ 或 $24$。
$\boxed{6}$ 或 $\boxed{24}$