《2025年辽宁作业分层培优学案八年级数学上册北师大版》

1. 下列 $ y $ 关于 $ x $ 的函数中,是正比例函数的为(C)
A.$ y = x^{2} + 1 $
B.$ y = \frac{2}{x} $
C.$ y = \frac{x}{2} $
D.$ y = \frac{x + 1}{2} $

答案： C

2. 下列函数：① $ y = 3x $；② $ y = 2x - 1 $；③ $ y = \frac{1}{x} $；④ $ y = x^{2} - 1 $；⑤ $ y = -\frac{x}{8} $。其中是一次函数的有(B)
A.4 个
B.3 个
C.2 个
D.1 个

答案： B

3. 已知函数 $ y = (m - 3)x^{m - 1} + 3 $ 是关于 $ x $ 的一次函数,则 $ m = $2。

答案： 2

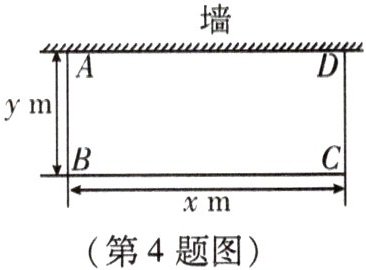
4. 如图是一边靠墙(墙足够长),其他三边用 $ 18m $ 篱笆围成的长方形蔬菜园 $ ABCD $,设 $ BC $ 边的长为 $ x m $,$ AB $ 边的长为 $ y m $。
(1) 写出 $ y $ 与 $ x $ 之间的关系式,并判断 $ y $ 是否为 $ x $ 的一次函数；
(2) 当 $ x = 6 $ 时,求 $ y $ 的值。

答案：
(1) 根据题意，篱笆总长为 $18m$，且一边靠墙，所以有：
$x + 2y = 18$，
从上式中解出 $y$，得到：
$y = 9 - \frac{x}{2} \quad (0 ＜ x \leq 18)$，
根据一次函数的定义，$y$ 是 $x$ 的一次函数。
(2) 将 $x = 6$ 代入 $y = 9 - \frac{x}{2}$ 中，得到：
$y = 9 - \frac{6}{2} = 9 - 3 = 6$，
所以，当 $x = 6$ 时，$y$ 的值为 $6m$。

5. 已知函数 $ y = (m - 2)x + (m^{2} - 4) $,
(1) 当 $ m $$\neq 2$时,这个函数是一次函数；
(2) 当 $ m = $$-2$时,这个函数是正比例函数。

答案：
(1) 一次函数的一般形式为 $ y = kx + b $（$ k \neq 0 $，$ k $、$ b $ 为常数）。对于函数 $ y = (m - 2)x + (m^2 - 4) $，要使其为一次函数，需满足 $ m - 2 \neq 0 $，解得 $ m \neq 2 $。
(2) 正比例函数是一次函数的特殊形式，即 $ b = 0 $ 且 $ k \neq 0 $。所以需满足：
$\begin{cases}m - 2 \neq 0 \\m^2 - 4 = 0\end{cases}$
由 $ m^2 - 4 = 0 $，得 $ m = \pm 2 $。又因为 $ m - 2 \neq 0 $，所以 $ m \neq 2 $，故 $ m = -2 $。
(1) $ \neq 2 $
(2) $ -2 $

6. 写出下列各题中 $ y $ 关于 $ x $ 的函数表达式,并判断：$ y $ 是否为 $ x $ 的一次函数？是否为正比例函数？
(1) 刚上市时西瓜每千克 $ 3.6 $ 元,买西瓜的总价 $ y $ 元与所买西瓜 $ x $ 千克之间的关系；
(2) 仓库内有粉笔 $ 400 $ 盒,如果每个星期领出 $ 36 $ 盒,仓库内余下的粉笔盒数 $ y $ 与星期数 $ x $ 之间的关系。

答案：
(1)根据总价等于单价乘数量，可得：
$y = 3.6x$
根据一次函数的定义，形如$y=kx+b$（$k$和$b$为常数，$k \ne 0$）的函数为一次函数，形如$y=kx$（$k$为常数，$k\ne 0$）的函数为正比例函数，正比例函数是一次函数的特殊形式。
所以$y$是$x$的一次函数，也是正比例函数。
(2)根据余下的数量等于原有的数量减去领出的数量，可得：
$y = 400 - 36x$
$y$是$x$的一次函数，不是正比例函数。

7. 一个漏水的水池,每过 $ 1min $ 水池的水位下降 $ 3cm $。
(1) 若开始时水池水位是 $ 60cm $,写出水池水位 $ y $(单位：$ cm $)与时间 $ t $(单位：$ min $)之间的关系式 $ y = kt + b $,并说明 $ k $ 和 $ b $ 的实际意义；
(2) 求水池水位降为 $ 0 $ 所需的时间。

答案：
(1) 根据题意，水位每分钟下降$3cm$，所以$k = -3$。
开始时，水池水位是$60cm$，所以$b = 60$。
因此，水池水位$y$与时间$t$之间的关系式为：$y = -3t + 60$。
其中，$k$表示水位随时间变化的速率，即每分钟下降$3cm$；$b$表示初始时刻的水位，即$60cm$。
(2)为了求水池水位降为$0$所需的时间，将$y$置为$0$并解方程：
$0 = -3t + 60$，
得$t = 20$。
所以，水池水位降为$0$所需的时间为$20min$。

8. 新定义：$[a,b]$ 为一次函数 $ y = ax + b(a \neq 0,a,b $ 为实数)的“关联数”。若“关联数”为 $[3,m - 2]$ 的一次函数是正比例函数,则点 $ (1 - m,1 + m) $ 在第二象限。

答案： 二