《2025年考点集训与满分备考七年级数学上册冀教版》

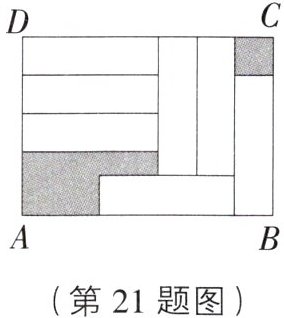
21. (7分)如图,7张全等的小长方形纸片(既不重叠也无空隙)放置于长方形$ABCD$中,设小长方形的长为$a$,宽为$b(a ＞ b)$,求两块阴影部分的周长和.

答案：
$4a$ [解析] 如图,延长$EF$,交$AB$于点$N$ 由题意可得$AD=BC=a+b$,$CG=b$,$CK=BC-BK=b$,由图知两块阴影部分的周长之和即长方形$MANF$和正方形$GHKC$的周长之和,所以两块阴影部分的周长和$=2[a+(a+b-3b)]+4b=2(a+a+b-3b)+4b=2a+2a+2b-6b+4b=4a$.

22. (9分)如图,在数轴上点$A表示数a$,点$B表示数b$,点$C表示数c$,数$a是多项式-2x^{2}-3x + 1$的一次项系数,数$b$是最大的负整数,数$c是单项式-\frac{1}{2}x^{2}y$的次数.

(1)$a = $-3,$b = $-1,$c = $3.
(2)点$A,B,C$开始在数轴上运动,若点$B和点C$分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,点$A$以每秒2个单位长度的速度向左运动,$t\ s$过后,若点$A与点B之间的距离表示为AB$,点$B与点C之间的距离表示为BC$,则$AB = $3t+2,$BC = $2t+4；(用含$t$的代数式表示)
(3)试问：$3BC - 2AB的值是否随着时间t$的变化而改变？若变化,请说明理由；若不变,请求出这个值.
不变，值为8。理由如下：$3BC - 2AB = 3(2t + 4) - 2(3t + 2) = 6t + 12 - 6t - 4 = 8$，计算结果为8，与$t$无关，故值不变。

答案：
(1)$-3$，$-1$，$3$；
(2)$3t+2$，$2t+4$；
(3)不变，值为$8$ [解析]
(1)$-3$ $-1$ $3$ 提示:$-2x^{2}-3x+1$的一次项是$-3x$,系数是$-3$,最大的负整数是$-1$,单项式$-\frac{1}{2}x^{2}y$的次数是$2+1=3$,所以$a=-3$,$b=-1$,$c=3$;
(2)$3t+2$ $2t+4$ 提示:点$A$以每秒2个单位长度的速度向左运动,所以运动后对应的点表示的数为$-3-2t$,点$B$以每秒1个单位长度的速度向右运动,所以运动后对应的点表示的数为$-1+t$,点$C$以每秒3个单位长度的速度向右运动,所以运动后对应的点表示的数为$3+3t$,所以$t\ s$后,$AB=|-1+t-(-3-2t)|=3t+2$;$BC=|3+3t-(-1+t)|=2t+4$;
(3)不变,理由如下:$3BC-2AB=3(2t+4)-2(3t+2)=6t+12-6t-4=8$.计算$3BC-2AB$的结果为8,与$t$无关,故值不变.

23. (10分)【阅读材料】“整体思想”是数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.如下是一道多项式求值的题：
代数式$x^{2}+x + 3$的值为7,则代数式$2x^{2}+2x - 3$的值为___.
【阅读理解】小明在做题时采用的方法如下：
由题意得$x^{2}+x + 3 = 7$,则有$x^{2}+x = 4$,
所以$2x^{2}+2x - 3 = 2(x^{2}+x)-3 = 2×4 - 3 = 5$.
所以代数式$2x^{2}+2x - 3$的值为5.
【解决问题】请运用小明的方法解决下列问题：
(1)若代数式$m^{2}-4m - 12$的值为0,求代数式$2m^{2}-8m - 8$的值；
(2)已知当$x = 2$时,代数式$ax^{5}+bx^{3}+2x - 1$的值为9,求当$x = -2$时,代数式$ax^{5}+bx^{3}+2x + 10$的值；
【拓展提升】
(3)若$x^{2}-xy = 80,xy - y^{2} = -20$,请直接写出代数式$x^{2}-2xy + y^{2}$的值.
(1)16
(2)0
(3)100

答案：
(1)$16$；
(2)$0$；
(3)$100$ [解析]
(1)因为$m^{2}-4m - 12=0$,所以$m^{2}-4m=12$,所以$2m^{2}-8m - 8=2(m^{2}-4m)-8=2×12 - 8=16$;
(2)因为$x=2$时,$ax^{5}+bx^{3}+2x - 1=9$,所以$ax^{5}+bx^{3}+2x=10$.当$x=-2$时,$ax^{5}+bx^{3}+2x=-10$,所以$ax^{5}+bx^{3}+2x + 10=-10 + 10=0$;
(3)因为$x^{2}-xy=80$,$xy - y^{2}=-20$,所以$x^{2}-xy-(xy - y^{2})=80-(-20)=100$,整理得$x^{2}-2xy + y^{2}=100$.