《2025年考点集训与满分备考七年级数学上册冀教版》

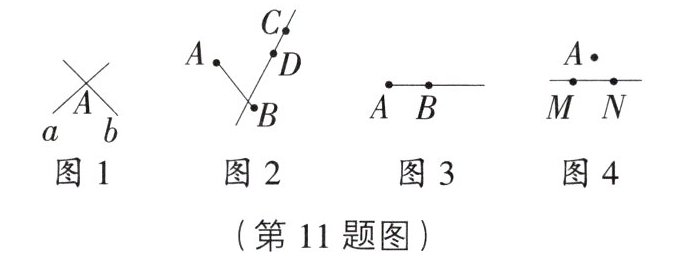
11. 下列几何图形与相应语言描述相符的有 (B)
①如图1,直线a,b相交于点A；
②如图2,直线CD与线段AB没有公共点；
③如图3,延长线段AB；
④如图4,直线MN经过点A。

A.1个
B.2个
C.3个
D.4个

答案： B [解析] ①题图1中，直线a和直线b相交于点A，语言描述与图相符，故①符合题意;②题图2中，直线CD与线段AB有公共点，语言描述与图不相符，故②不符合题意;③题图3中，延长线段AB，语言描述与图相符，故③符合题意;④题图4中，直线MN不经过点A，语言描述与图不相符，故④不符合题意。综上，与相应语言描述相符的有2个。

12. 下列语句描述正确的有 (C)
①直线MN和直线NM是同一条直线；
②射线AB和射线BA是同一条射线；
③线段PQ和线段QP是同一条线段；
④直线上的任意一点都可以把该直线分成两条射线。
A.①②③
B.①②④
C.①③④
D.②③④

答案： C [解析] ①③④正确;②不正确，两者端点不同。

13. 真实情境值日生小明想把教室桌椅摆放整齐,为了将一列课桌对齐,他把这列课桌的最前面一张和最后面一张先拉成一条线,其余课桌按这条直线摆放,这样做用到的数学知识是两点确定一条直线。

答案： 两点确定一条直线

14. 易错题如图,点A,B,C,D,E,F在同一条直线上,则图中线段和射线的条数分别为(C)

A.10,10
B.12,15
C.15,12
D.15,15

答案： C [解析] 题图中线段有15条:线段AB、线段AC、线段AD、线段AE、线段AF、线段BC、线段BD、线段BE、线段BF、线段CD、线段CE、线段CF、线段DE、线段DF、线段EF;以每个点为端点的射线有2条，共6个点，故射线有12条。

15. 生活情境如图,由A站始发终点至D站的某一次列车,运行途中停靠的车站依次是A—B—C—D,那么要为这次列车制作的单程火车票种数是 (B)

A.4
B.6
C.10
D.12

答案： B [解析] 单程火车票两个站点有一种票，相当于两两组合，根据$\frac{n(n - 1)}{2}$计算有$\frac{4×(4 - 1)}{2}=6$(种)，所以要为这次列车制作的单程火车票有6种。

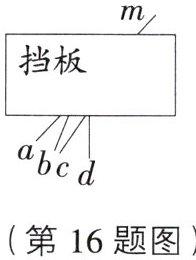
16. 如图,已知四条线段a,b,c,d中的一条与挡板另一侧的线段m在同一直线上,请借助直尺判断该线段是 ( )

A.a
B.b
C.c
D.d

答案：
A [解析] 利用直尺画出图形如下，可以看出线段a与m在一条直线上。

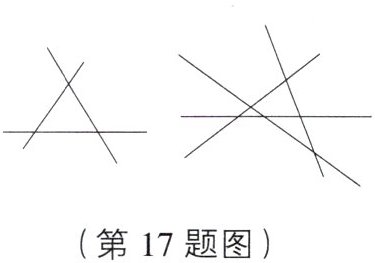
17. 如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有190个交点。

答案： 190 [解析] 2条直线相交有1个交点，3条直线两两相交最多有1+2=3(个)交点，4条直线两两相交最多有1+2+3=6(个)交点，……，n条直线两两相交最多有$\frac{n(n - 1)}{2}$个交点，所以20条直线两两相交最多有190个交点。

18. 中考新考法结论开放A,B,C,D四点如图所示,按要求作出图形(不写作法)并回答问题。
(1)连接AC,BD交于点O,并作直线AD与射线AB；

(2)写出图形中出现的线段(至少写出6条)。

答案：
[解析]
(1)如图所示;
(2)图形中出现的线段有:线段AB、线段AD、线段AC、线段AO、线段BO、线段BD、线段CO、线段DO(任选6条线段即可)。