第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11. 一个人手里拿着一个绑在一根棍上的半圆面,当这个人把这个半圆面绕着这根棍飞快地旋转起来时就会看到一个球,这种现象说明
面动成体
。
答案:
面动成体
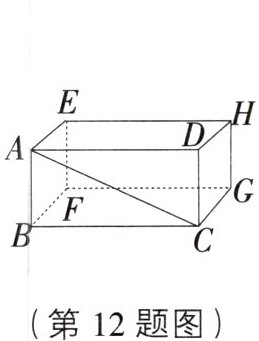
12. 如图,一只蚂蚁从长方体的一个顶点A沿表面爬行到顶点C处,有多条爬行路线,其中沿AC爬行一定是最短路线,其依据的数学道理是
两点之间线段最短
。
答案:
两点之间线段最短 [解析]因为蚂蚁从长方体的一个顶点A沿表面爬行到顶点C处有多个爬行路线,只有AC是直线段,所以沿AC爬行一定是最短路线,其数学道理是两点之间线段最短.
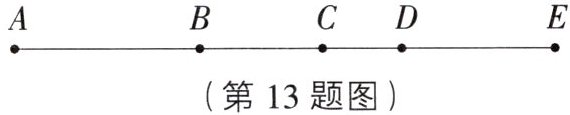
13. 如图,B,C,D是线段AE上的三点,已知AE= 9.4 cm,BD= 2 cm,则图中以A,B,C,D,E这五点为端点的所有线段长度之和为
41.6
cm。
答案:
41.6 [解析]因为AE=9.4cm,BD=2cm,所以以A、B、C、D、E这5个点为端点的所有线段的和为AB+AC+AD+AE+BC+BD+BE+CD+CE+DE=(BC+CD)+(AB+BE)+(AC+CE)+(AD+DE)+AE+BD=BD+AE+AE+AE+AE+BD=2+9.4+9.4+9.4+9.4+2=41.6(cm).
14. 新定义若$∠α的度数是∠β$的度数的n倍,则$∠α叫做∠β$的n倍角。
(1)若$∠M= 20^{\circ}22'$,则$∠M$的3倍角的度数为
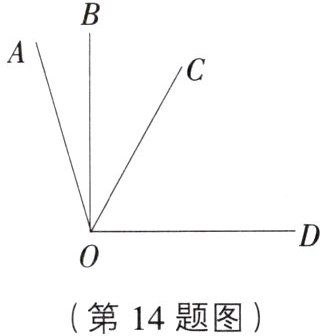
(2)如图,若$∠AOC是∠AOB$的3倍角,$∠COD是∠AOB$的4倍角,且$∠BOD= 90^{\circ}$,则$∠BOC$的度数为______。
(1)若$∠M= 20^{\circ}22'$,则$∠M$的3倍角的度数为
61°6′
;(2)如图,若$∠AOC是∠AOB$的3倍角,$∠COD是∠AOB$的4倍角,且$∠BOD= 90^{\circ}$,则$∠BOC$的度数为______。

30°
答案:
(1)61°6′
(2)30° [解析]
(1)因为∠M=20°22',所以3∠M=3×20°22'=61°6';
(2)因为∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,所以设∠AOB=α,则∠AOC=3α,∠COD=4α,所以∠AOD=7α,所以∠BOD=6α.因为∠BOD=90°,所以α=15°,所以∠BOC=90°−4×15°=30°.
(1)61°6′
(2)30° [解析]
(1)因为∠M=20°22',所以3∠M=3×20°22'=61°6';
(2)因为∠AOC是∠AOB的3倍角,∠COD是∠AOB的4倍角,所以设∠AOB=α,则∠AOC=3α,∠COD=4α,所以∠AOD=7α,所以∠BOD=6α.因为∠BOD=90°,所以α=15°,所以∠BOC=90°−4×15°=30°.
15. (6分)运算能力计算。
(1)$108^{\circ}18'-56^{\circ}23'$;
(2)$180^{\circ}-(34^{\circ}54'+21^{\circ}33')$;
(3)$182^{\circ}36'÷4+22^{\circ}16'×3$。
(1)$108^{\circ}18'-56^{\circ}23'$;
(2)$180^{\circ}-(34^{\circ}54'+21^{\circ}33')$;
(3)$182^{\circ}36'÷4+22^{\circ}16'×3$。
答案:
[解析]
(1)108°18′−56°23'=51°55’;
(2)180°−(34°54'+21°33′)=180°−56°27′=123°33′;
(3)182°36'÷4+22°16'×3=45°39′+66°48'=112°27′.
(1)108°18′−56°23'=51°55’;
(2)180°−(34°54'+21°33′)=180°−56°27′=123°33′;
(3)182°36'÷4+22°16'×3=45°39′+66°48'=112°27′.
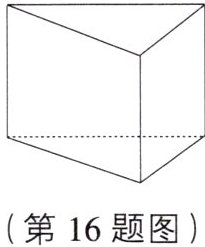
16. (6分)如图所示的图形是一个棱柱,请问:
(1)这个棱柱由几个面围成?各面的交线有几条?它们是直的还是曲的?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?
(1)这个棱柱由几个面围成?各面的交线有几条?它们是直的还是曲的?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?

答案:
[解析]
(1)这个棱柱由5个面围成,各面的交线有9条,这9条线都是直的;
(2)这个棱柱的两个底面都是三角形,三个侧面都是长方形;
(3)该棱柱有6个顶点.
(1)这个棱柱由5个面围成,各面的交线有9条,这9条线都是直的;
(2)这个棱柱的两个底面都是三角形,三个侧面都是长方形;
(3)该棱柱有6个顶点.
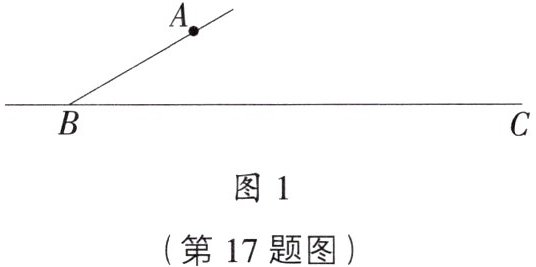
17. (6分)作图题:
(1)利用尺规作图(保留作图痕迹即可):如图1,在射线BC上,作线段BD,使BD= 2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC= ∠ABC;
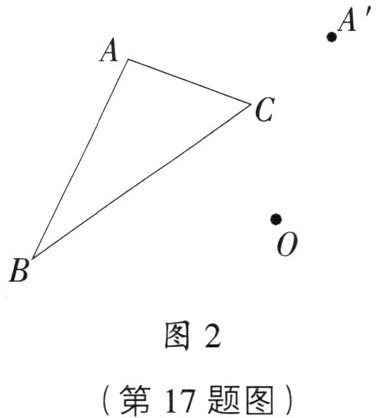
(2)如图2,三角形ABC绕点O旋转,顶点A的对应点为$A'$,请画出旋转后的图形。
(1)利用尺规作图(保留作图痕迹即可):如图1,在射线BC上,作线段BD,使BD= 2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC= ∠ABC;

(2)如图2,三角形ABC绕点O旋转,顶点A的对应点为$A'$,请画出旋转后的图形。

答案:
[解析]
(1)如图1所示,线段BD,∠EDC和∠E'DC即所求;
(2)将三角形ABC绕点O旋转,顶点A的对应点为A',则旋转角是∠AOA',连接OB,在OB上方作∠B'OB=∠AOA',OB'=OB,找到点B的对应点B',同理,找到点C的对应点C',顺次连接A'、B'、C',画出旋转后的图形,如图2.
[解析]
(1)如图1所示,线段BD,∠EDC和∠E'DC即所求;

(2)将三角形ABC绕点O旋转,顶点A的对应点为A',则旋转角是∠AOA',连接OB,在OB上方作∠B'OB=∠AOA',OB'=OB,找到点B的对应点B',同理,找到点C的对应点C',顺次连接A'、B'、C',画出旋转后的图形,如图2.

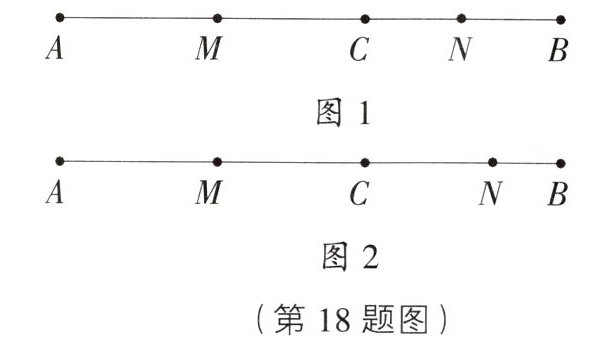
18. (8分)已知点C在线段AB上,AC= 8 cm,CB= 6 cm,M为线段AC的中点。
(1)如图1,若N为线段CB的中点,求线段MN的长;
(2)如图2,若N为线段CB上的点,且满足2CN= 3NB,求线段MN的长。
(1)如图1,若N为线段CB的中点,求线段MN的长;
(2)如图2,若N为线段CB上的点,且满足2CN= 3NB,求线段MN的长。

答案:
[解析]
(1)因为M为线段AC的中点,N为线段CB的中点,所以MC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4(cm),CN=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3(cm),所以MN=MC+CN=4+3=7(cm);
(2)因为M为线段AC的中点,所以MC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4(cm).因为2CN=3NB,所以CN=$\frac{3}{5}$BC=3.6cm,所以MN=MC+CN=4+3.6=7.6(cm).
(1)因为M为线段AC的中点,N为线段CB的中点,所以MC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4(cm),CN=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3(cm),所以MN=MC+CN=4+3=7(cm);
(2)因为M为线段AC的中点,所以MC=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4(cm).因为2CN=3NB,所以CN=$\frac{3}{5}$BC=3.6cm,所以MN=MC+CN=4+3.6=7.6(cm).
查看更多完整答案,请扫码查看


