第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
7. 如图,数轴上点$A$,$B$,$C$,$D所表示的数分别是a$,$b$,$c$,$d$,若$abcd<0$,$ab>cd$,则原点的位置在(
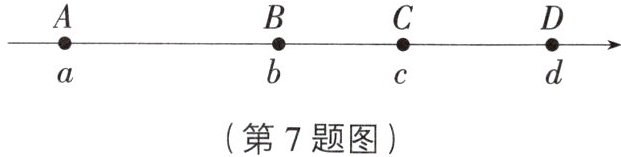
A.点$A$的左边
B.线段$AB$上
C.线段$BC$上
D.线段$CD$上
D
)
A.点$A$的左边
B.线段$AB$上
C.线段$BC$上
D.线段$CD$上
答案:
D [解析] 因为abcd<0,所以a<0,b>0,c>0,d>0,或a<0,b<0,c<0,d>0.又因为ab>cd,所以a<0,b<0,c<0,d>0,所以原点的位置在线段CD上.
8. 下面计算正确的是(
A.$(-5)×(-4)×(-2)×(-2)= 80$
B.$(-12)×(\frac{1}{3}-\frac{1}{4}-1)= 0$
C.$(-9)×5×(-4)×0= 180$
D.$(-2)×5-2×(-1)-(-2)×2= -8$
A
)A.$(-5)×(-4)×(-2)×(-2)= 80$
B.$(-12)×(\frac{1}{3}-\frac{1}{4}-1)= 0$
C.$(-9)×5×(-4)×0= 180$
D.$(-2)×5-2×(-1)-(-2)×2= -8$
答案:
A [解析] A.(-5)×(-4)×(-2)×(-2)=5×4×2×2=80,故本选项正确;B.(-12)×(1/3 - 1/4 - 1)=-4 + 3 + 12=11,故本选项错误;C.(-9)×5×(-4)×0=0,故本选项错误;D.(-2)×5 - 2×(-1)-(-2)×2=(-2)×(5 - 1 - 2)=-4,故本选项错误.
9. 在数$-6$,$2$,$-3$,$5$,$-2$中任取三个数相乘,其中最小的积是$a$,最大的积是$b$,则$a+b$的结果是(
A.$54$
B.$30$
C.$24$
D.$0$
30
)A.$54$
B.$30$
C.$24$
D.$0$
答案:
B [解析] 由题意,得a=(-6)×2×5=-60,b=(-6)×(-3)×5=90,则a + b=-60 + 90=30.
10. 计算:$(-24)×(\frac{7}{12}+\frac{3}{4}-\frac{5}{6})= $
-12
。
答案:
-12 [解析] 解法一:原式=(-24)×7/12 + (-24)×3/4 - (-24)×5/6=-14 - 18 + 20=-12;解法二:原式=(-24)×1/2=-12.
11. 定义一种新的运算:$x★y= (x+2)×(y+2)$。
(1)计算$(-3)★(-4)$;
(2)计算$[(-3)★(-4)]★(-5)与(-3)★[(-4)★(-5)]$,此运算满足乘法结合律吗?
(1)计算$(-3)★(-4)$;
(2)计算$[(-3)★(-4)]★(-5)与(-3)★[(-4)★(-5)]$,此运算满足乘法结合律吗?
答案:
[解析]
(1)(-3)★(-4)=(-3 + 2)×(-4 + 2)=-1×(-2)=2;
(2)[(-3)★(-4)]★(-5)=[(-3 + 2)×(-4 + 2)]★(-5)=2★(-5)=(2 + 2)×(-5 + 2)=4×(-3)=-12;
(-3)★[(-4)★(-5)]=(-3)★[(-4 + 2)×(-5 + 2)]=(-3)★[(-2)×(-3)]=(-3)★6=(-3 + 2)×(6 + 2)=-1×8=-8,所以[(-3)★(-4)]★(-5)≠(-3)★[(-4)★(-5)],所以此运算不满足乘法结合律.
(1)(-3)★(-4)=(-3 + 2)×(-4 + 2)=-1×(-2)=2;
(2)[(-3)★(-4)]★(-5)=[(-3 + 2)×(-4 + 2)]★(-5)=2★(-5)=(2 + 2)×(-5 + 2)=4×(-3)=-12;
(-3)★[(-4)★(-5)]=(-3)★[(-4 + 2)×(-5 + 2)]=(-3)★[(-2)×(-3)]=(-3)★6=(-3 + 2)×(6 + 2)=-1×8=-8,所以[(-3)★(-4)]★(-5)≠(-3)★[(-4)★(-5)],所以此运算不满足乘法结合律.
12. 嘉嘉玩一个摸球游戏,在一个密闭的容器中放入五个标有如图所示的数字的小球,先从容器中摸取几个小球,然后把摸到的球上的数字进行乘法运算。
(1)若取出的四个小球上分别标有$+2$,$-8$,$0$,$-3$,求$(+2)×(-8)×0×(-3)$的值;
(2)若取出的四个小球上的四个数字的积不为$0$,求这四个数字的积;
(3)若取出的三个小球上的三个数字的积最大,求最大的积。
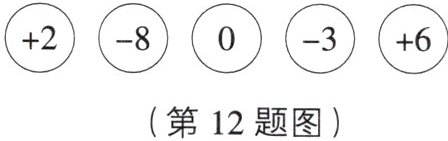
(1)若取出的四个小球上分别标有$+2$,$-8$,$0$,$-3$,求$(+2)×(-8)×0×(-3)$的值;
(2)若取出的四个小球上的四个数字的积不为$0$,求这四个数字的积;
(3)若取出的三个小球上的三个数字的积最大,求最大的积。

答案:
[解析]
(1)(+2)×(-8)×0×(-3)=0;
(2)因为这四个数字的积不为0,所以没有抽到标0的小球,所以这四个数字的积为(+2)×(-8)×(-3)×(+6)=2×8×3×6=288;
(3)当抽到-8,-3,+6时,三个数字的积最大,所以三个数字最大的积为(-8)×(-3)×(+6)=144.
(1)(+2)×(-8)×0×(-3)=0;
(2)因为这四个数字的积不为0,所以没有抽到标0的小球,所以这四个数字的积为(+2)×(-8)×(-3)×(+6)=2×8×3×6=288;
(3)当抽到-8,-3,+6时,三个数字的积最大,所以三个数字最大的积为(-8)×(-3)×(+6)=144.
13. 计算$(-1)×(-1)×(-1)$的结果是(
A.$-1$
B.$1$
C.$-3$
D.$3$
A
)A.$-1$
B.$1$
C.$-3$
D.$3$
答案:
A
14. 在学习有理数的乘法时,李老师和同学们做了这样一个游戏:将$2024$这个数说给第一名同学,第一名同学将它减去它的$\frac{1}{2}$的结果告诉第二名同学,第二名同学再将听到的结果减去它的$\frac{1}{3}$的结果告诉第三名同学,第三名同学再将听到的结果减去它的$\frac{1}{4}$的结果告诉第四名同学……照这样的方法直到全班$40$名同学全部传完,最后一名同学将听到的结果告诉李老师。你知道最后的结果吗?
答案:
[解析] 由题意,可得2024×(1 - 1/2)×(1 - 1/3)×(1 - 1/4)×…×(1 - 1/40)=2024×1/2×2/3×3/4×…×39/40=2024/40=253/5.
查看更多完整答案,请扫码查看


