第89页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 教材P150,T5·习题改编 多项式 $ 2x - xy + y $ 与另一个多项式的差是 $ 3xy - x $,则这个多项式是(
A.$ 3x - 4xy + y $
B.$ 2x - 4xy $
C.$ -2xy + y $
D.$ x - 2xy + y $
A
)A.$ 3x - 4xy + y $
B.$ 2x - 4xy $
C.$ -2xy + y $
D.$ x - 2xy + y $
答案:
A [解析]由题意可得这个多项式为2x-xy+y-(3xy-x)=2x-xy+y-3xy+x=3x-4xy+y.
2. 教材P150,T2·习题变式 当 $ x = -4 $ 时,代数式 $ -x^3 - 4x^2 - 2 $ 与 $ x^3 + 5x^2 + 3x - 4 $ 的和是(
A.0
B.4
C.-4
D.-2
D
)A.0
B.4
C.-4
D.-2
答案:
D [解析]代数式-x³-4x²-2与x³+5x²+3x-4的和是(-x³-4x²-2)+(x³+5x²+3x-4)=x²+3x-6,当x=-4时,原式=(-4)²+3×(-4)-6=-2.
3. 已知一个多项式与 $ x^2 - xy $ 的和是 $ 2x^2 + xy + 3y^2 $,求这个多项式。
答案:
[解析]这个多项式为(2x²+xy+3y²)-(x²-xy)=2x²+xy+3y²-x²+xy=x²+2xy+3y².
4. 若多项式 $ xy^2 - 6x^2 - 2kxy - 6 $ 与 $ y^2 + 6xy $ 的和中不含 $ xy $ 项,则 $ k $ 的值为(
A.3
B.6
C.-3
D.-6
3
)A.3
B.6
C.-3
D.-6
答案:
A [解析]xy²-6x²-2kxy-6+y²+6xy=xy²-6x²+y²+(6-2k)xy-6,因为多项式中不含xy项,所以6-2k=0,所以k=3.
5. 整体代入法 已知整式 $ x^2y $ 的值是 2,则 $ 5x^2y + 5xy - 7x - (4x^2y + 5xy - 7x) $ 的值是(
A.$ \frac{1}{2} $
B.-2
C.2
D.4
C
)A.$ \frac{1}{2} $
B.-2
C.2
D.4
答案:
C [解析]因为x²y=2,所以原式=5x²y+5xy-7x-4x²y-5xy+7x=x²y=2.
6. 老师设计了接力游戏,用合作的方式完成化简代数式,规则是:每名同学只能利用前面一名同学的式子,进一步计算,再将结果传给下一名同学,最后解决问题。过程如图所示,接力中,自己负责的一步正确的是(
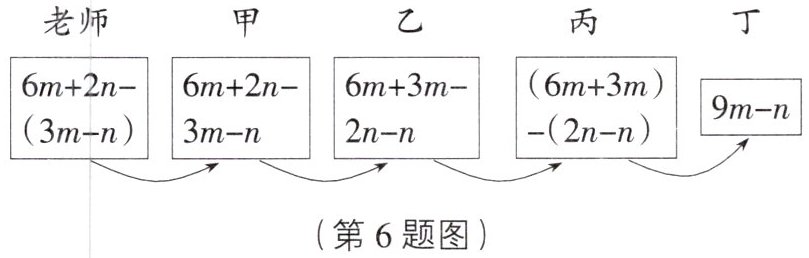
A.甲
B.乙
C.丙
D.丁
D
)
A.甲
B.乙
C.丙
D.丁
答案:
D [解析]由老师到甲,甲接力应为6m+2n-(3m-n)=6m+2n-3m+n,故甲错误;由甲到乙,乙接力应为6m+2n-3m-n=6m-3m+2n-n,故乙错误;由乙到丙,丙接力应为6m+3m-2n-n=(6m+3m)-(2n+n),故丙错误;由丙到丁,丁接力应为(6m+3m)-(2n-n)=9m-n,故丁正确.
7. 新定义 定义:若 $ a + b = ab $,则称 $ a $,$ b $ 是“西溪数”,例如:$ 3 + 1.5 = 3×1.5 $,因此 3 和 1.5 是一组“西溪数”。若 $ m $,$ n $ 是一组“西溪数”,则 $ 2mn - (3mn - m - n - 6) $ 的值为
6
。
答案:
6 [解析]因为m,n是一组“西溪数”,所以m+n=mn,则原式=2mn-3mn+m+n+6=-mn+m+n+6=-(m+n)+m+n+6=6.
8. 代数推理 观察等式:$ 2 + 2^2 = 2^3 - 2 $,$ 2 + 2^2 + 2^3 = 2^4 - 2 $,$ 2 + 2^2 + 2^3 + 2^4 = 2^5 - 2 $,…,已知按一定规律排列的一组数 $ 2^{100} $,$ 2^{101} $,$ 2^{102} $,…,$ 2^{199} $。若 $ 2^{100} = m $,用含 $ m $ 的代数式表示这组数的和是
m²-m
。(注:$ 2^{200} = (2^{100})^2 = m^2 $)
答案:
m²-m [解析]因为2+2²=2³-2,2+2²+2³=2⁴-2,2+2²+2³+2⁴=2⁵-2,…,所以第n个等式为2+2²+2³+…+2ⁿ⁺¹=2ⁿ⁺²-2,所以2+2²+2³+…+2¹⁹⁹=2²⁰⁰-2,2+2²+2³+…+2⁹⁹=2¹⁰⁰-2,所以2¹⁰⁰+2¹⁰¹+2¹⁰²+…+2¹⁹⁹=(2+2²+2³+…+2¹⁹⁹)-(2+2²+2³+…+2⁹⁹)=2²⁰⁰-2-(2¹⁰⁰-2)=2²⁰⁰-2¹⁰⁰,因为2¹⁰⁰=m,2²⁰⁰=(2¹⁰⁰)²=m²,所以2¹⁰⁰+2¹⁰¹+2¹⁰²+…+2¹⁹⁹=m²-m.
9. 运算能力 化简:$ 3x^2 + 2xy - 4y^2 - (3xy - 4y^2 + 3x^2) $。
答案:
[解析]3x²+2xy-4y²-(3xy-4y²+3x²)=3x²+2xy-4y²-3xy+4y²-3x²=-xy.
10. 先化简,再求值:$ 4(a^2 - 2ab) - (3a^2 - 5ab + 1) $,其中 $ a = -2 $,$ b = \frac{1}{3} $。
答案:
[解析]原式=4a²-8ab-3a²+5ab-1=a²-3ab-1,当a=-2,b=1/3时,原式=(-2)²-3×(-2)×1/3-1=4+2-1=5.
11. 无关型问题 已知代数式 $ A = 6x + 4y - 5 $,$ B = 2(x + y) + (x - 3) $。
(1)当 $ x = y = -2 $ 时,求 $ A - B $ 的值;
(2)请问 $ A - 2B $ 的值与 $ x $,$ y $ 的取值是否有关?试说明理由。
(1)当 $ x = y = -2 $ 时,求 $ A - B $ 的值;
(2)请问 $ A - 2B $ 的值与 $ x $,$ y $ 的取值是否有关?试说明理由。
答案:
(1)-12;
(2)A-2B的值与x,y的取值无关.理由如下:因为A-2B=6x+4y-5-2[2(x+y)+(x-3)]=6x+4y-5-[4(x+y)+2(x-3)]=6x+4y-5-(4x+4y+2x-6)=6x+4y-5-4x-4y-2x+6=1,所以A-2B的值与x,y的取值无关.
(1)-12;
(2)A-2B的值与x,y的取值无关.理由如下:因为A-2B=6x+4y-5-2[2(x+y)+(x-3)]=6x+4y-5-[4(x+y)+2(x-3)]=6x+4y-5-(4x+4y+2x-6)=6x+4y-5-4x-4y-2x+6=1,所以A-2B的值与x,y的取值无关.
查看更多完整答案,请扫码查看


