第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 根据如图所示的运算程序计算 $ y $ 的值,若输入 $ m = - 2 $,$ n = 2 $,则输出 $ y $ 的值是(
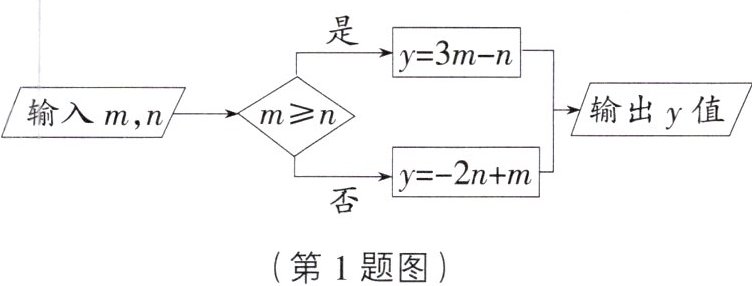
A.$ 8 $
B.$ 6 $
C.$ - 6 $
D.$ - 8 $
C
)
A.$ 8 $
B.$ 6 $
C.$ - 6 $
D.$ - 8 $
答案:
C [解析]因为-2<2,即m<n,所以y=-2n+m=-2×2-2=-6.
2. 教材P119,T2·练习高仿 已知 $ a = - 8 $,$ b = 3 $,$ c = 2 $,$ d = - 4 $,求下面各式的值:
(1)$ a - b + c - d $;
(2)$ a - ( b + c + d ) $.
(1)$ a - b + c - d $;
(2)$ a - ( b + c + d ) $.
答案:
[解析]
(1)a-b+c-d=-8-3+2-(-4)=-5;
(2)a-(b+c+d)=-8-[3+2+(-4)]=-8-1=-9.
(1)a-b+c-d=-8-3+2-(-4)=-5;
(2)a-(b+c+d)=-8-[3+2+(-4)]=-8-1=-9.
3. 若 $ x = - 2 $,$ y = 1 $,则代数式 $ x ^ { 2 } - x y - 1 $ 的值为
5
.
答案:
5 [解析]当x=-2,y=1时,x²-xy-1=(-2)²-(-2)×1-1=4+2-1=5.
4. 当 $ x = - 1 $,$ y = 3 $ 时,代数式 $ x ^ { 3 } - 2 y $ 的值为(
A.$ - 7 $
B.$ - 5 $
C.$ 4 $
D.$ 7 $
A
)A.$ - 7 $
B.$ - 5 $
C.$ 4 $
D.$ 7 $
答案:
A [解析]当x=-1,y=3时,x³-2y=(-1)³-2×3=-1-6=-7.
5. 整体代入法 若 $ x - 2 y $ 的值为 $ 2 $,则代数式 $ - 3 ( x - 2 y ) + 5 $ 的值是(
A.$ - 6 $
B.$ - 1 $
C.$ 2 $
D.$ 5 $
B
)A.$ - 6 $
B.$ - 1 $
C.$ 2 $
D.$ 5 $
答案:
B [解析]因为x-2y的值为2,即x-2y=2,所以-3(x-2y)+5=-3×2+5=-6+5=-1.
6. 流程图 根据流程图中的运算程序,当输入数字 $ x $ 为 $ 27 $ 时,第 $ 2024 $ 次输出的数字 $ y $ 为(
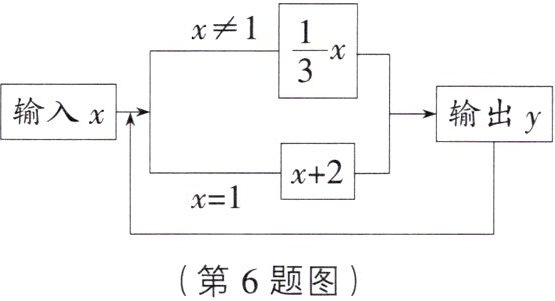
A.$ 3 $
B.$ 9 $
C.$ 27 $
D.$ 1 $
A
)
A.$ 3 $
B.$ 9 $
C.$ 27 $
D.$ 1 $
答案:
A [解析]当x=27时,第1次输出结果为y=27×$\frac{1}{3}$=9,第2次输出结果为y=9×$\frac{1}{3}$=3,第3次输出结果为y=3×$\frac{1}{3}$=1,第4次输出结果为y=1+2=3,第5次输出结果为y=3×$\frac{1}{3}$=1,……,所以从第3次开始,第奇数次输出结果为1,第偶数次输出结果为3.因为2024是偶数,所以第2024次输出的数字y为3.
7. 直接代入法 在 $ - 1 $,$ 0 $,$ 1 $,$ 2 $,$ 3 $,$ 4 $ 这六个数中,能使代数式 $ x ( x + 1 ) ( x - 2 ) ( x - 6 ) $ 的值为零的有(
A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个
B
)A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个
答案:
B [解析]将-1,0,1,2,3,4这六个数分别代入代数式进行验证,能使代数式的值为零的有3个,即-1,0,2.
8. 当 $ x = \pm 1 $ 时,代数式 $ 5 x ^ { 4 } - 6 x ^ { 2 } - 2 $ 的值(
A.互为相反数
B.相等
C.互为倒数
D.异号
B
)A.互为相反数
B.相等
C.互为倒数
D.异号
答案:
B [解析]因为当x=1时,原式=5×1⁴-6×1²-2=5-6-2=-3;当x=-1时,原式=5×(-1)⁴-6×(-1)²-2=5-6-2=-3,所以当x=±1时,代数式5x⁴-6x²-2的值相等.
9. 下列代数式,满足表中条件的是(

A.$ - x - 3 $
B.$ 2 x - 3 $
C.$ x ^ { 2 } + 2 x - 3 $
D.$ x ^ { 2 } - 2 x - 3 $
B
)
A.$ - x - 3 $
B.$ 2 x - 3 $
C.$ x ^ { 2 } + 2 x - 3 $
D.$ x ^ { 2 } - 2 x - 3 $
答案:
B
10. 若代数式 $ x ^ { 2 } - 2 x - 6 $ 的值为 $ 0 $,则代数式 $ 2 ( x ^ { 2 } - 2 x - 1 ) $ 的值等于
10
.
答案:
10 [解析]因为代数式x²-2x-6的值为0,所以代数式x²-2x的值为6,则2(x²-2x-1)=2×(6-1)=2×5=10.
11. 如图,已知 $ a > 0 $,$ b > 0 $,若 $ a + 2 b = 6 $,$ a ^ { 2 } + 4 b ^ { 2 } = 20 $,请借助图直观分析,计算 $ a b $ 的值.
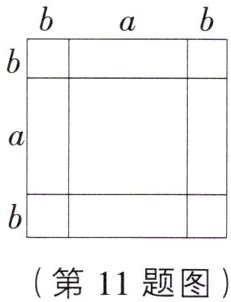

答案:
[解析]由题图可知,小正方形的边长为b,长方形的长为a、宽为b,
∵a+2b=6,
∴大正方形的边长为6,
∴大正方形的面积为36.
∵a²+4b²=20,
∴20+4ab=36,
∴ab=$\frac{36-20}{4}$=4.
∵a+2b=6,
∴大正方形的边长为6,
∴大正方形的面积为36.
∵a²+4b²=20,
∴20+4ab=36,
∴ab=$\frac{36-20}{4}$=4.
查看更多完整答案,请扫码查看


