第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
12. 如图,小明设计了一个计算程序,并按此程序进行了计算,若开始输入的数为-7,则最后输出的数为

-18
.
答案:
-18 [解析]$(-7)+7+(-8)+2+(-12)=-18.$
13. 如图,在一条不完整的数轴上从左到右有A,B,C三点,它们分别表示三个不同的有理数,其中点A到点B的距离为3个单位长度,点B到点C的距离为8个单位长度,设点A,B,C所表示的三个有理数的和是m.
(1)若以A为原点,则数轴上点B所表示的数是
(2)若以C为原点,再添上一个有理数n,使得这四个有理数的和为0,求n的值.
(3)若原点在图中数轴上,且点B到原点的距离为4个单位长度,求m的值.
(2)因为C为原点,点B到点C的距离为8且点B在点C左侧,所以点B表示的数为-8;点A到点B的距离为3且点A在点B左侧,所以点A表示的数为-8-3=-11。已知四个有理数的和为0,即-11+(-8)+0+n=0,解得n=19。
(3)因为点B到原点的距离为4,所以点B表示的数为4或-4。
当点B表示4时,点A在点B左侧且距离为3,所以点A表示4-3=1;点C在点B右侧且距离为8,所以点C表示4+8=12,此时m=1+4+12=17。
当点B表示-4时,点A在点B左侧且距离为3,所以点A表示-4-3=-7;点C在点B右侧且距离为8,所以点C表示-4+8=4,此时m=-7+(-4)+4=-7。
综上,m的值为-7或17。
(1)若以A为原点,则数轴上点B所表示的数是
3
;若以B为原点,则m的值为5
.(2)若以C为原点,再添上一个有理数n,使得这四个有理数的和为0,求n的值.
(3)若原点在图中数轴上,且点B到原点的距离为4个单位长度,求m的值.
(2)因为C为原点,点B到点C的距离为8且点B在点C左侧,所以点B表示的数为-8;点A到点B的距离为3且点A在点B左侧,所以点A表示的数为-8-3=-11。已知四个有理数的和为0,即-11+(-8)+0+n=0,解得n=19。
(3)因为点B到原点的距离为4,所以点B表示的数为4或-4。
当点B表示4时,点A在点B左侧且距离为3,所以点A表示4-3=1;点C在点B右侧且距离为8,所以点C表示4+8=12,此时m=1+4+12=17。
当点B表示-4时,点A在点B左侧且距离为3,所以点A表示-4-3=-7;点C在点B右侧且距离为8,所以点C表示-4+8=4,此时m=-7+(-4)+4=-7。
综上,m的值为-7或17。
答案:
[解析]
(1)3 5提示:因为A为原点,点A到点B的距离为3,点B到点C的距离为8,所以数轴上点B所表示的数是3.若以B为原点,则点A所表示的数为-3,点C所表示的数为8,所以$m=-3+0+8=5.$
(2)因为C为原点,所以点A所表示的数为-11,点B所表示的数为-8,所以$-11-8+0+n=0,-19+n=0$,根据两个互为相反数的数相加的和为0,可得$n=19.$
(3)因为点A到点B的距离为3,点B到点C的距离为8,点B到原点的距离为4,所以当原点在点B的左边时,A,B,C三点在数轴上所对应的数分别为1,4,12,所以$m=1+4+12=17$.当原点在点B的右边时,A,B,C三点在数轴上所对应的数分别为-7,-4,4,所以$m=-7-4+4=-7.$综上所述,m的值为-7或17.
(1)3 5提示:因为A为原点,点A到点B的距离为3,点B到点C的距离为8,所以数轴上点B所表示的数是3.若以B为原点,则点A所表示的数为-3,点C所表示的数为8,所以$m=-3+0+8=5.$
(2)因为C为原点,所以点A所表示的数为-11,点B所表示的数为-8,所以$-11-8+0+n=0,-19+n=0$,根据两个互为相反数的数相加的和为0,可得$n=19.$
(3)因为点A到点B的距离为3,点B到点C的距离为8,点B到原点的距离为4,所以当原点在点B的左边时,A,B,C三点在数轴上所对应的数分别为1,4,12,所以$m=1+4+12=17$.当原点在点B的右边时,A,B,C三点在数轴上所对应的数分别为-7,-4,4,所以$m=-7-4+4=-7.$综上所述,m的值为-7或17.
14. 在某场足球比赛中,根据场上攻守形势,守门员会在门前来回跑动,若以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,+12,-6,-9,+4,-14.(开始计时时,守门员在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离是多少米?
(3)若守门员离开球门线的距离超过10m(不包括10m),则对方球员挑射极可能造成破门,则在这一时间段内,对方球员有几次挑射破门的机会?
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离是多少米?
(3)若守门员离开球门线的距离超过10m(不包括10m),则对方球员挑射极可能造成破门,则在这一时间段内,对方球员有几次挑射破门的机会?
答案:
[解析]
(1)$10+(-2)+5+12+(-6)+(-9)+4+(-14)=0$,所以守门员最后正好回到球门线上;
(2)第一次10 m,第二次$10-2=8(m),$第三次$8+5=13(m),$第四次$13+12=25(m),$第五次$25-6=19(m),$第六次$19-9=10(m),$第七次$10+4=14(m),$第八次$14-14=0(m),$因为$25>19>14>13>10>8>0,$所以守门员离开球门线的最远距离是25 m;
(3)在第三次、第四次、第五次和第七次有挑射破门的机会,所以对方球员有四次挑射破门的机会.
(1)$10+(-2)+5+12+(-6)+(-9)+4+(-14)=0$,所以守门员最后正好回到球门线上;
(2)第一次10 m,第二次$10-2=8(m),$第三次$8+5=13(m),$第四次$13+12=25(m),$第五次$25-6=19(m),$第六次$19-9=10(m),$第七次$10+4=14(m),$第八次$14-14=0(m),$因为$25>19>14>13>10>8>0,$所以守门员离开球门线的最远距离是25 m;
(3)在第三次、第四次、第五次和第七次有挑射破门的机会,所以对方球员有四次挑射破门的机会.
15. 如图,比数轴上点A表示的数大3的数是(

A.-1
B.0
C.1
D.2
D
)
A.-1
B.0
C.1
D.2
答案:
D [解析]由数轴可得,点A表示的有理数是-1,则比数轴上点A表示的数大3的数是$(-1)+3=2.$
16. 我国是最早认识负数,并进行相关运算的国家,在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(-4)=-1的过程,按照这种方法,图2表示的过程应是在计算(
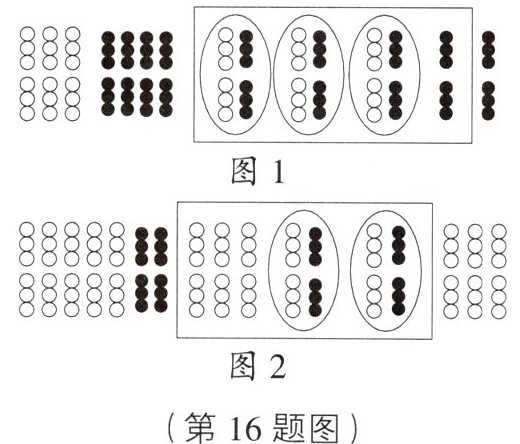
A.(-5)+2=-3
B.(-5)+(-2)=-7
C.5+2=7
D.5+(-2)=3
D
)
A.(-5)+2=-3
B.(-5)+(-2)=-7
C.5+2=7
D.5+(-2)=3
答案:
D
查看更多完整答案,请扫码查看


