第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
9. 分类讨论法 数轴上有一点 $ P $ 从原点出发向正方向移动 4 个单位长度恰好与点 $ A $ 重合,此时数轴上的点 $ B $ 与点 $ A $ 的距离是 4 个单位长度,则点 $ B $ 表示的数是(
A.8
B.0
C.8 或 0
D.-8 或 0
8或0
)A.8
B.0
C.8 或 0
D.-8 或 0
答案:
9.C [解析]由题意得,点A表示的数为4,因为数轴上的点B与点A的距离是4个单位长度,所以点B所表示的数为4+4=8或4-4=0,即8或0.
10. 规律探究 等边三角形 $ ABC $ 在数轴上的位置如图所示,点 $ A $, $ C $ 对应的数分别为 0 和 -1,若三角形 $ ABC $ 绕顶点沿顺时针方向在数轴上连续翻转,翻转 1 次后,点 $ B $ 所对应的数为 1,则连续翻转若干次后,数 2 024 对应的点为(

A.点 $ A $
B.点 $ B $
C.点 $ C $
D.不确定
C
)
A.点 $ A $
B.点 $ B $
C.点 $ C $
D.不确定
答案:
10.C [解析]因为翻转1次后,数1对应的点为B,翻转2次后,数2对应的点为C,翻转3次后,数3对应的点为A,翻转4次后,数4对应的点为B,……,所以点的变化周期为3.又因为2024÷3=674……2,所以连续翻转2024次后,数2024对应的点为C.
11. 小红在做作业时,不小心将墨水洒在一条数轴上.如图,根据图中标出的数值,判断被墨渍盖住的整数共有
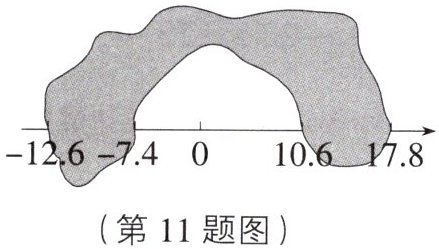
12
个.
答案:
11.12 [解析]根据数轴的特点,-12.6到-7.4之间的整数有-12,-11,-10,-9,-8;10.6到17.8之间的整数有11,12,13,14,15,16,17,所以被墨渍盖住的整数共有12个.
12. 较难题 如图,在一条可以折叠的数轴上, $ A $ 和 $ B $ 表示的数分别是 -9 和 6,点 $ C $ 为 $ A $, $ B $ 之间一点(不与 $ A $, $ B $ 重合),以点 $ C $ 为折点,将此数轴向右对折,且 $ AB = 1 $,则点 $ C $ 表示的数是
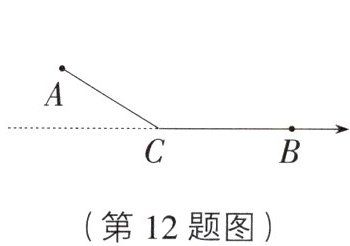
-1或-2
.
答案:
12.-1或-2 [解析]因为点A表示的数为-9,点B表示的数为6,所以对折前AB=6+9=15.因为对折后AB=1,所以对折后当点A在点B的左边时,点A表示的数是5,此时点C表示的数为-2;对折后当点A在点B的右边时,点A表示的数是7,此时点C表示的数为-1.
13. 应用意识 快递员骑车从公司出发,先向西骑行 3 km 到达 $ A $ 地,继续向西骑行 4 km 到达 $ B $ 地,然后向东骑行 9 km 到达 $ C $ 地,最后回到公司.
(1)以公司为原点,向东为正方向,以 1 km 为 1 个单位长度画出数轴,并在该数轴上表示出 $ A $, $ B $, $ C $ 三地的位置.
(2)$ C $ 地离 $ A $ 地有多远?
(3)快递员一共骑行了多少千米?
(1)以公司为原点,向东为正方向,以 1 km 为 1 个单位长度画出数轴,并在该数轴上表示出 $ A $, $ B $, $ C $ 三地的位置.
(2)$ C $ 地离 $ A $ 地有多远?
(3)快递员一共骑行了多少千米?
答案:
13.[解析]
(1)A,B,C三地的位置如图所示;
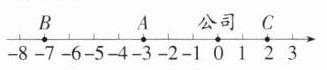
(2)由数轴可知,C地离A地的距离为2+3=5(km);
(3)由数轴可知,3+4+9+2=18(km).答:快递员一共骑行了18 km.
13.[解析]
(1)A,B,C三地的位置如图所示;
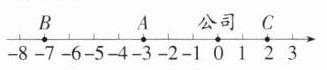
(2)由数轴可知,C地离A地的距离为2+3=5(km);
(3)由数轴可知,3+4+9+2=18(km).答:快递员一共骑行了18 km.
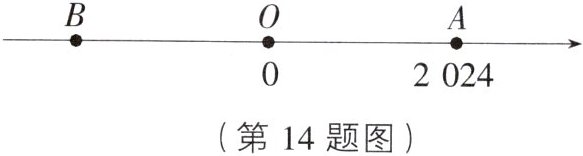
14. 数形结合法 如图,数轴上点 $ A $ 表示的数是 2 024,点 $ B $ 到原点的距离与点 $ A $ 到原点的距离相等,则点 $ B $ 表示的数是(
A.2 024
B.-2 024
C.$ \frac{1}{2 024} $
D.$ - \frac{1}{2 024} $
-2024
)
A.2 024
B.-2 024
C.$ \frac{1}{2 024} $
D.$ - \frac{1}{2 024} $
答案:
14.B [解析]因为OA=OB,点A表示的数是2024,所以OB=2024.因为点B在数轴的负半轴上,所以点B表示的数为-2024.
15. 中考新考法 数形结合法 如图,直径为 $ \frac{2}{\pi} $ 个单位长度的圆片上有一点 $ A $ 与数轴上的原点重合.
(1)把圆片沿数轴向左滚动 1 周,点 $ A $ 到达数轴上点 $ C $ 的位置,点 $ C $ 对应的数是
(2)圆片从点 $ A $ 出发沿数轴同一方向滚动 2 周,点 $ A $ 到达数轴上点 $ D $ 的位置,点 $ D $ 对应的数是
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,滚动 5 次的情况记录如下:+2,-1,+3,-4,-3.当圆片结束滚动时,点 $ A $ 对应的数是多少?

(1)把圆片沿数轴向左滚动 1 周,点 $ A $ 到达数轴上点 $ C $ 的位置,点 $ C $ 对应的数是
-2
;(2)圆片从点 $ A $ 出发沿数轴同一方向滚动 2 周,点 $ A $ 到达数轴上点 $ D $ 的位置,点 $ D $ 对应的数是
4或-4
;(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,滚动 5 次的情况记录如下:+2,-1,+3,-4,-3.当圆片结束滚动时,点 $ A $ 对应的数是多少?

圆片共向右滚动2+3=5(周),共向左滚动1+4+3=8(周),8-5=3(周),所以当圆片结束滚动时,相当于圆片向左滚动了3周.因为$\pi×\frac{2}{\pi}×3=6$,所以圆片结束滚动时,点A对应的数是-6.
答案:
15.[解析]
(1)-2
(2)4或-4 提示:因为$\pi×\frac{2}{\pi}=2$,所以把圆片沿数轴向左滚动2周,点D对应的数是-4;把圆片沿数轴向右滚动2周,点D对应的数是4.
(3)圆片共向右滚动2+3=5(周),共向左滚动1+4+3=8(周),8-5=3(周),所以当圆片结束滚动时,相当于圆片向左滚动了3周.因为$\pi×\frac{2}{\pi}×3=6$,所以圆片结束滚动时,点A对应的数是-6.
(1)-2
(2)4或-4 提示:因为$\pi×\frac{2}{\pi}=2$,所以把圆片沿数轴向左滚动2周,点D对应的数是-4;把圆片沿数轴向右滚动2周,点D对应的数是4.
(3)圆片共向右滚动2+3=5(周),共向左滚动1+4+3=8(周),8-5=3(周),所以当圆片结束滚动时,相当于圆片向左滚动了3周.因为$\pi×\frac{2}{\pi}×3=6$,所以圆片结束滚动时,点A对应的数是-6.
查看更多完整答案,请扫码查看


