《2025年考点集训与满分备考七年级数学上册冀教版》

1. 若一列数：1,4,16,64,…,按照这种规律,第n个数是$4^{n-1}$。(用含n的代数式表示)

答案： $4^{n-1}$ [解析]因为第1个数是1=$4^{0}=4^{1-1}$,第2个数是4=$4^{1}=4^{2-1}$,第3个数是16=$4^{2}=4^{3-1}$,第4个数是64=$4^{3}=4^{4-1}$,……,所以第n个数是$4^{n-1}$.

2. 教材P116,T1·习题高仿 如图所示的是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n(n是正整数)个图案由3n+1个基础图形组成。

答案： (3n+1) [解析]根据题意可得,第1个图案基础图形个数为1+3×1=4,第2个图案基础图形个数为1+3×2=7,第3个图案基础图形个数为1+3×3=10,……,第n个图案基础图形个数为1+3×n=3n+1.

3. 如图所示的图案均由长度相同的小木棒按一定的规律拼搭而成：第1个图案需7根小木棒,第2个图案需13根小木棒,……,依此规律,第11个图案所需木棒根数为(157)

A.156
B.157
C.158
D.159

答案： B [解析]根据题意可知,第1个图案需7根小木棒,即7=1×(1+3)+3,第2个图案需13根小木棒,即13=2×(2+3)+3,第3个图案需21根小木棒,即21=3×(3+3)+3,……则第11个图案需11×(11+3)+3=157(根)小木棒.

4. 观察下列式子,探究其规律：$-2x$,$4x^{2}$,$-6x^{3}$,$8x^{4}$,$-10x^{5}$,$12x^{6}$,…,按照上述规律,第n个式子是($(-1)^{n}2nx^{n}$)
A.$(-1)^{n}2nx^{n}$
B.$(-1)^{n + 1}2nx^{n}$
C.$2nx^{n}$
D.$(-1)^{n}2nx^{n + 1}$

答案： A [解析]因为第1个式子是-2x=$(-1)^{1}×(2×1)x^{1}$,第2个式子是4$x^{2}$=$(-1)^{2}×(2×2)x^{2}$,第3个式子是-6$x^{3}$=$(-1)^{3}×(2×3)x^{3}$,第4个式子是8$x^{4}$=$(-1)^{4}×(2×4)x^{4}$,……所以第n个式子是$(-1)^{n}2nx^{n}$.

5. 观察下列一组数：$-\frac{2}{3}$,$\frac{4}{5}$,$-\frac{6}{7}$,$\frac{8}{9}$,$-\frac{10}{11}$,…,它们是按一定规律排列的,那么这一组数的第n个数是(D)
A.$\frac{2n}{2n + 1}$
B.$(-1)^{n}\frac{2n}{2n - 1}$
C.$\frac{n + 1}{n + 2}$
D.$(-1)^{n}\frac{2n}{2n + 1}$

答案： D [解析]因为第1个数为$-\frac{2}{3}=(-1)^{1}×\frac{2×1}{2×1+1}$,第2个数为$\frac{4}{5}=(-1)^{2}×\frac{2×2}{2×2+1}$,第3个数为$-\frac{6}{7}=(-1)^{3}×\frac{2×3}{2×3+1}$,……,所以第n个数为$(-1)^{n}\frac{2n}{2n+1}$.方法点拨本题属于数字变化规律中的数字为分数的情况,解答此类题时,要分别找到分子与分母的变化规律,然后用代数式表示这一规律.

6. 观察下列算式：$2^{1}= 2$,$2^{2}= 4$,$2^{3}= 8$,$2^{4}= 16$,$2^{5}= 32$,$2^{6}= 64$,$2^{7}= 128$,$2^{8}= 256$,…,$3^{1}= 3$,$3^{2}= 9$,$3^{3}= 27$,$3^{4}= 81$,$3^{5}= 243$,$3^{6}= 729$,$3^{7}= 2187$,$3^{8}= 6561$,…。根据上述算式中的规律,$2^{21}+3^{11}$的末位数字是(9)
A.3
B.5
C.7
D.9

答案： D [解析]因为$2^{1}=2$,$2^{2}=4$,$2^{3}=8$,$2^{4}=16$,$2^{5}=32$,$2^{6}=64$,$2^{7}=128$,$2^{8}=256$,…,所以其结果的末位数字每4次运算尾数循环出现.因为21÷4=5……1,所以$2^{21}$的末位数字与$2^{1}=2$的尾数相同,为2.因为$3^{1}=3$,$3^{2}=9$,$3^{3}=27$,$3^{4}=81$,$3^{5}=243$,$3^{6}=729$,$3^{7}=2187$,$3^{8}=6561$,…,所以其结果的末位数字每4次运算尾数循环出现,因为11÷4=2……3,所以$3^{11}$的末位数字与$3^{3}=27$的尾数相同,为7,所以$2^{21}+3^{11}$的末位数字是9.

7. 按规律排列的一列数：2,5,8,11,…,第n个数是3n-1。

答案： 3n-1 [解析]因为2=3×1-1,5=3×2-1,8=3×3-1,11=3×4-1,…,所以第n个数为3n-1.

8. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第7个图形需要63个黑色棋子。

答案： 63 [解析]第1个图形中黑色棋子的个数是3=1×3,第2个图形中黑色棋子的个数是8=2×4,第3个图形中黑色棋子的个数是15=3×5,……,按照此规律可得第7个图形中黑色棋子的个数是7×(7+2)=63.

9. 如图是按规律排列的一组图形,观察图形解答下列问题：

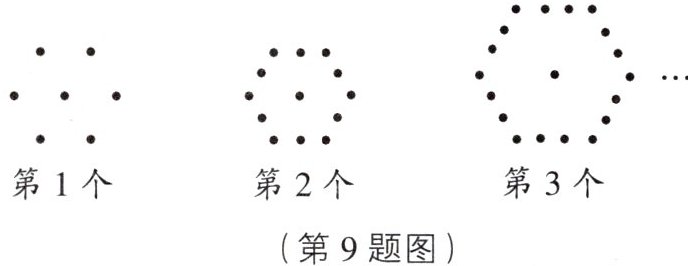
(1)第5个图形中一共有多少个点？
(2)请用含n的代数式表示出第n个图形中点的数量。

答案：
(1)第5个图形中一共有31个点;
(2)6n+1.