第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 一电子跳蚤在数轴上从原点开始,第 1 次向右跳 1 个单位长度,紧接着第 2 次向左跳 2 个单位长度,第 3 次向右跳 3 个单位长度,第 4 次向左跳 4 个单位长度,……,依此规律跳下去,当它跳第 2024 次落下时,落点处表示的数为(
A.-2024
B.2024
C.-1012
D.1012
C
)A.-2024
B.2024
C.-1012
D.1012
答案:
C [解析]因为第1次向右跳1个单位长度,紧接着第2次向左跳2个单位长度,第3次向右跳3个单位长度,第4次向左跳4个单位长度,……,所以第1次和第2次跳完后向左移动1个单位长度,第3次和第4次跳完后向左移动1个单位长度,……,因为2024÷2=1012,所以它跳第2024次落下时,向左移动1012个单位长度.
2. 观察下列一组数:-2,$\frac{4}{3}$,-$\frac{8}{5}$,$\frac{16}{7}$,-$\frac{32}{9}$,…,它们是按照一定规律排列的,那么这组数的第 $n$ 个数是(
A.-$\frac{2^{n}}{2n + 1}$
B.$\frac{(-2)^{n}}{2n + 1}$
C.$\frac{(-2)^{n}}{2n - 1}$
D.$\frac{-2^{n}}{2n - 1}$
$\frac{(-2)^n}{2n-1}$
)A.-$\frac{2^{n}}{2n + 1}$
B.$\frac{(-2)^{n}}{2n + 1}$
C.$\frac{(-2)^{n}}{2n - 1}$
D.$\frac{-2^{n}}{2n - 1}$
答案:
C [解析]由$-2,\frac {4}{3},-\frac {8}{5},\frac {16}{7},$$-\frac {32}{9},...$,可得$-\frac {2}{1},\frac {4}{3},-\frac {8}{5},\frac {16}{7},$$-\frac {32}{9},...$,所以第n个数是$\frac {(-2)^{n}}{2n-1}.$
3. 计算:$3^{1}+1= 4$,$3^{2}+1= 10$,$3^{3}+1= 28$,$3^{4}+1= 82$,$3^{5}+1= 244$,…,归纳计算结果中的个位数字的规律,猜测 $3^{2025}+1$ 的结果中的个位数字是(
A.0
B.2
C.4
D.8
4
)A.0
B.2
C.4
D.8
答案:
C [解析]由题知,计算结果中的个位数字以4,0,8,2循环出现,因为$2025÷4=506... ... 1$,所以$3^{2025}+1$的结果中的个位数字为4.
4. 如图,观察点阵图的规律,第 100 个图的小黑点的个数应该是(
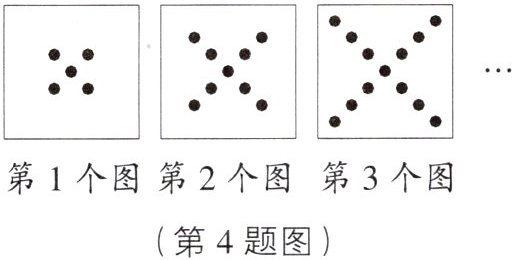
A.399
B.400
C.401
D.402
401
)
A.399
B.400
C.401
D.402
答案:
C [解析]因为第1个图形中小黑点的个数为$1+4×1=5$,第2个图形中小黑点的个数为$1+4×2=9$,第3个图形中小黑点的个数为$1+4×3=13$,……,所以第100个图形中小黑点的个数为$1+4×100=401.$
5. 如图,观察下列一组图形,其中图 1 中共有 2 颗星,图 2 中共有 6 颗星,图 3 中共有 11 颗星,图 4 中共有 17 颗星,……,按此规律,图 10 中星星的颗数是(

A.62
B.68
C.74
D.87
74
)
A.62
B.68
C.74
D.87
答案:
C [解析]设图n中星星的颗数是$a_{n}$(n为正整数),因为$a_{1}=2=$$\frac {1×(1+1)}{2}+1,a_{2}=6=\frac {2×(2+1)}{2}+3,$$a_{3}=11=\frac {3×(3+1)}{2}+5,$$a_{4}=17=\frac {4×(4+1)}{2}+7,$所以$a_{n}=\frac {n(n+1)}{2}+(2n-1),$所以$a_{10}=\frac {10×(10+1)}{2}+(2×10-1)=74.$
6. 如图所示的图案是用长度相同的火柴按一定规律拼搭而成的,第 1 个图案需 8 根火柴,第 2 个图案需 15 根火柴,……,按此规律,第 10 个图案需要的火柴数量是(

A.72 根
B.78 根
C.71 根
D.74 根
71
)
A.72 根
B.78 根
C.71 根
D.74 根
答案:
C [解析]因为第1个图案需8根火柴,第2个图案需15根火柴,$8+7×$$(2-1)=15$,第3个图案需22根火柴,$8+7×(3-1)=22$,……,所以第10个图案需$8+7×(10-1)=71$(根)火柴.
7. 如图,将一枚跳棋放在七边形 $ABCDEFG$ 的顶点 $A$ 处,按顺时针方向移动这枚跳棋 2025 次。移动规则:第 $k$ 次移动 $k$ 个顶点(如第一次移动 1 个顶点,跳棋停留在 $B$ 处,第二次移动 2 个顶点,跳棋停留在 $D$ 处),按这样的规则,在这 2025 次移动后,跳棋停留的顶点是(

A.$A$
B.$B$
C.$D$
D.$G$
D
)
A.$A$
B.$B$
C.$D$
D.$G$
答案:
C [解析]根据题意得第1次到第7次移动后跳棋停留的顶点分别是B,D,G,D,B,A,A,跳棋停留的顶点7次一个循环,$2025÷7=289... ... 2,$故第2025次移动后停留的顶点是D.
查看更多完整答案,请扫码查看


