第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
13. $\frac{2}{3}$的倒数是
$\frac{3}{2}$
.
答案:
$\frac{3}{2}$
14. 计算$0.75^2×(-\frac{4}{3})$的结果是
$-\frac{3}{4}$
.
答案:
$-\frac{3}{4}$
15. 如图,数轴(单位长度为1)上有三个点A,B,C,若点A,B表示的数互为相反数.
(1)图中点C表示的数是______;
(2)若点D在数轴上,且CD= 3,则点D表示的数为______.

(1)图中点C表示的数是______;
(2)若点D在数轴上,且CD= 3,则点D表示的数为______.

答案:
(1)1
(2)-2或4
[解析]
(1)因为点A,B表示的数互为相反数,如图,则点O的位置即为原点的位置,所以点C表示的数为1;
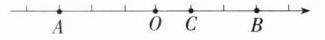
(2)由
(1)知,点C表示的数为1,因为CD的长度为3,所以当点D在点C左侧时,点D表示的数为1-3=-2;当点D在点C右侧时,点D表示的数为1+3=4.综上,点D表示的数为-2或4.
(1)1
(2)-2或4
[解析]
(1)因为点A,B表示的数互为相反数,如图,则点O的位置即为原点的位置,所以点C表示的数为1;
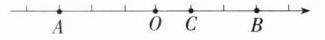
(2)由
(1)知,点C表示的数为1,因为CD的长度为3,所以当点D在点C左侧时,点D表示的数为1-3=-2;当点D在点C右侧时,点D表示的数为1+3=4.综上,点D表示的数为-2或4.
16. 新定义 对于有理数a,b,定义一种新运算“⊗”,规定a⊗b= |a+b|-|a-b|.如3⊗5= |3+5|-|3-5|= 8-2= 6.
(1)3⊗(-5)的值为
(2)若$(a+2)^2+$|b-1|= 0,则a⊗b=
(1)3⊗(-5)的值为
-6
;(2)若$(a+2)^2+$|b-1|= 0,则a⊗b=
-2
.
答案:
(1)-6
(2)-2 [解析]
(1)因为$a\otimes b=|a+b|-|a-b|$,所以$3\otimes (-5)=|3-5|-|3-(-5)|=2-8=-6$;
(2)因为$(a+2)^2+|b-1|=0$,所以$(a+2)^2=0$,$|b-1|=0$,所以a=-2,b=1.所以$a\otimes b=|-2+1|-|-2-1|=1-3=-2$.
(1)-6
(2)-2 [解析]
(1)因为$a\otimes b=|a+b|-|a-b|$,所以$3\otimes (-5)=|3-5|-|3-(-5)|=2-8=-6$;
(2)因为$(a+2)^2+|b-1|=0$,所以$(a+2)^2=0$,$|b-1|=0$,所以a=-2,b=1.所以$a\otimes b=|-2+1|-|-2-1|=1-3=-2$.
17. (5分)若有理数a,b,c满足:$(a-1)^2+(2-b)^4+$|3c+1|= 0.求(c-a)^2+c^3-b的值.
答案:
[解析]因为$(a-1)^2+(2-b)^4+|3c+1|=0$,所以a-1=0,2-b=0,3c+1=0,所以$a=1$,$b=2$,$c=-\frac{1}{3}$,所以$(c-a)^2+c^3-b=(-\frac{1}{3}-1)^2+(-\frac{1}{3})^3-2=-\frac{7}{27}$.
18. (12分)运算能力 计算.
(1)(-6)-(+5)+(-9)+(-4)-(-9);
(2)3.75+(-5.18)-(-2.25)+5.18;
(3)|$-2\frac{1}{2}$|÷|$1\frac{1}{4}$|×(-4);
$(4)-1^{2024}-(1-0.5)×\frac{1}{3};$
$(5)(\frac{1}{2}+\frac{2}{3}-\frac{3}{4}-\frac{11}{12})÷\frac{1}{24};$
$(6)(-3)×(-4)+16÷(-2)^3×(-1)^{2024}-$| -5 |.
(1)(-6)-(+5)+(-9)+(-4)-(-9);
(2)3.75+(-5.18)-(-2.25)+5.18;
(3)|$-2\frac{1}{2}$|÷|$1\frac{1}{4}$|×(-4);
$(4)-1^{2024}-(1-0.5)×\frac{1}{3};$
$(5)(\frac{1}{2}+\frac{2}{3}-\frac{3}{4}-\frac{11}{12})÷\frac{1}{24};$
$(6)(-3)×(-4)+16÷(-2)^3×(-1)^{2024}-$| -5 |.
答案:
[解析]
(1)原式=-6-5-9-4+9=(-6-5-4)+(-9+9)=(-15)+0=-15;
(2)原式=3.75-5.18+2.25+5.18=(3.75+2.25)+(5.18-5.18)=6;
(3)原式=$(-\frac{5}{2})×\frac{4}{5}×(-4)=\frac{5}{2}×\frac{4}{5}×4=8$;
(4)原式=$-1-\frac{1}{2}×\frac{1}{3}=-1-\frac{1}{6}=-1\frac{1}{6}$;
(5)原式=$(\frac{1}{2}+\frac{2}{3}-\frac{3}{4}-\frac{11}{12})×24=\frac{1}{2}×24+\frac{2}{3}×24-\frac{3}{4}×24-\frac{11}{12}×24=12+16-18-22=-12$;
(6)原式=$3×4+16÷(-8)×1-5=12-2×1-5=12-2-5=5$.
(1)原式=-6-5-9-4+9=(-6-5-4)+(-9+9)=(-15)+0=-15;
(2)原式=3.75-5.18+2.25+5.18=(3.75+2.25)+(5.18-5.18)=6;
(3)原式=$(-\frac{5}{2})×\frac{4}{5}×(-4)=\frac{5}{2}×\frac{4}{5}×4=8$;
(4)原式=$-1-\frac{1}{2}×\frac{1}{3}=-1-\frac{1}{6}=-1\frac{1}{6}$;
(5)原式=$(\frac{1}{2}+\frac{2}{3}-\frac{3}{4}-\frac{11}{12})×24=\frac{1}{2}×24+\frac{2}{3}×24-\frac{3}{4}×24-\frac{11}{12}×24=12+16-18-22=-12$;
(6)原式=$3×4+16÷(-8)×1-5=12-2×1-5=12-2-5=5$.
19. (8分)缺项题 嘉淇在解一道数学计算题时,发现有一个数被污染了.
计算:(-1)^3×■-(1-3)÷4,
(1)若嘉淇猜污染的数为1,请计算(-1)^3×1-(1-3)÷4;
(2)老师说嘉淇猜错了,正确的计算结果是$\frac{5}{2},$求被污染的数是多少.
计算:(-1)^3×■-(1-3)÷4,
(1)若嘉淇猜污染的数为1,请计算(-1)^3×1-(1-3)÷4;
(2)老师说嘉淇猜错了,正确的计算结果是$\frac{5}{2},$求被污染的数是多少.
答案:
[解析]
(1)$(-1)^3×1-(1-3)÷4=-1-(-2)÷4=-1+\frac{1}{2}=-\frac{1}{2}$;
(2)由题意,得$[\frac{5}{2}+(1-3)÷4]÷(-1)^3=[\frac{5}{2}+(-2)÷4]÷(-1)=[\frac{5}{2}+(-\frac{1}{2})]÷(-1)=2÷(-1)=-2$,即被污染的数是-2.
(1)$(-1)^3×1-(1-3)÷4=-1-(-2)÷4=-1+\frac{1}{2}=-\frac{1}{2}$;
(2)由题意,得$[\frac{5}{2}+(1-3)÷4]÷(-1)^3=[\frac{5}{2}+(-2)÷4]÷(-1)=[\frac{5}{2}+(-\frac{1}{2})]÷(-1)=2÷(-1)=-2$,即被污染的数是-2.
查看更多完整答案,请扫码查看


