第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 教材 P88,T2·练习变式 如图,把一副三角板叠合在一起,则∠AOB的度数是 (
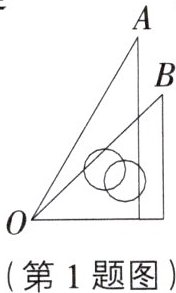
A.15°
B.20°
C.30°
D.70°
A
)
A.15°
B.20°
C.30°
D.70°
答案:
A [解析]由图形可知,∠AOB=60°-45°=15°.
2. 教材 P87 例·例题高仿 计算:
(1)38°24'+23°47';
(2)131°28'-51°32'15".
(1)38°24'+23°47';
(2)131°28'-51°32'15".
答案:
[解析]
(1)38°24'+23°47'=61°71'=62°11';
(2)131°28'-51°32'15''=79°55'45''.
(1)38°24'+23°47'=61°71'=62°11';
(2)131°28'-51°32'15''=79°55'45''.
3. 教材 P89,T5·习题高仿 如图,∠AOC=90°,OC平分∠DOB,且∠DOC=25°35',则∠BOA的度数是 (

A.64°65'
B.54°65'
C.64°25'
D.54°25'
C
)
A.64°65'
B.54°65'
C.64°25'
D.54°25'
答案:
C [解析]因为 OC 平分∠DOB,所以∠BOC=∠DOC=25°35'.因为∠AOC=90°,所以∠BOA=∠AOC-∠BOC=90°-25°35'=64°25'.
4. 如图,OB是∠AOC的平分线,OC是∠BOD的平分线,给出下列说法:①∠AOD=3∠BOC;②∠AOD=2∠AOC;③∠AOC=2∠COD,其中不正确的是______.(只填序号)


②
答案:
② [解析]因为 OB 是∠AOC 的平分线,OC 是∠BOD 的平分线,所以∠AOB=∠BOC=∠COD=$\frac{1}{3}$∠AOD,所以∠AOD=3∠BOC,∠AOD=1.5∠AOC,∠AOC=2∠COD,故①③正确,②错误.
5. 教材 P89,T2·习题变式 已知∠α=42°12',与∠α互余的角的度数是 (
A.132°12'
B.137°48'
C.57°48'
D.47°48'
D
)A.132°12'
B.137°48'
C.57°48'
D.47°48'
答案:
D [解析]因为∠α=42°12',所以与∠α互余的角的度数是 90°-42°12'=89°60'-42°12'=47°48'.
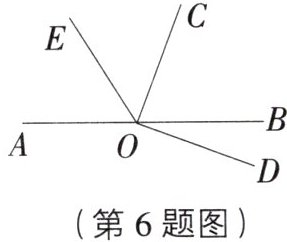
6. 如图,∠AOC与∠BOC互为补角,∠BOC与∠BOD互为余角,且∠BOC=4∠BOD.
(1)求∠BOC的度数;
(2)若OE平分∠AOC,求∠BOE的度数.
(1)求∠BOC的度数;
(2)若OE平分∠AOC,求∠BOE的度数.

答案:
[解析]
(1)因为∠BOC 与∠BOD 互为余角,所以∠BOC+∠BOD=90°.因为∠BOC=4∠BOD,所以∠BOC=$\frac{4}{5}$×90°=72°;
(2)因为∠AOC 与∠BOC 互为补角,所以∠AOC+∠BOC=180°.所以∠AOC=180°-∠BOC=180°-72°=108°.因为 OE 平分∠AOC,所以∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×108°=54°,所以∠BOE=∠COE+∠BOC=54°+72°=126°.
(1)因为∠BOC 与∠BOD 互为余角,所以∠BOC+∠BOD=90°.因为∠BOC=4∠BOD,所以∠BOC=$\frac{4}{5}$×90°=72°;
(2)因为∠AOC 与∠BOC 互为补角,所以∠AOC+∠BOC=180°.所以∠AOC=180°-∠BOC=180°-72°=108°.因为 OE 平分∠AOC,所以∠COE=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×108°=54°,所以∠BOE=∠COE+∠BOC=54°+72°=126°.
7. 已知∠AOB=58°32',以O为端点作射线OC,使∠AOC=42°41',则∠BOC的度数为 ( )
A.15°51'
B.101°13'
C.15°51'或101°13'
D.16°51'或101°13'
A.15°51'
B.101°13'
C.15°51'或101°13'
D.16°51'或101°13'
答案:
C [解析]分两种情况,射线 OC 在∠AOB 外部或内部.如图 1,当射线 OC 在∠AOB 外部时,∠BOC=∠AOB+∠AOC=58°32'+42°41'=101°13';如图 2,当射线 OC 在∠AOB 内部时,∠BOC=∠AOB-∠AOC=58°32'-42°41'=15°51'.所以∠BOC 的度数是 101°13'或 15°51'.

C [解析]分两种情况,射线 OC 在∠AOB 外部或内部.如图 1,当射线 OC 在∠AOB 外部时,∠BOC=∠AOB+∠AOC=58°32'+42°41'=101°13';如图 2,当射线 OC 在∠AOB 内部时,∠BOC=∠AOB-∠AOC=58°32'-42°41'=15°51'.所以∠BOC 的度数是 101°13'或 15°51'.


8. 三角板中角度计算问题 如图,将一块三角板中60°角的顶点与另一块三角板的直角顶点重合,若∠1=28°10',则∠2的大小是 (

A.28°10'
B.31°50'
C.61°50'
D.58°10'
D
)
A.28°10'
B.31°50'
C.61°50'
D.58°10'
答案:
D [解析]由图可知∠2=90°-(60°-∠1)=90°-60°+∠1=30°+∠1,因为∠1=28°10',所以∠2=30°+28°10'=58°10'.
查看更多完整答案,请扫码查看


