第80页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 设$x$是用字母表示的有理数,则下列各式中必大于零的是(
A.$x + 2$
B.$2x$
C.$|x|$
D.$x^2 + 2$
D
)A.$x + 2$
B.$2x$
C.$|x|$
D.$x^2 + 2$
答案:
D
2. 用$a$表示的数一定是(
A.正数
B.正数或负数
C.正整数
D.以上全不对
D
)A.正数
B.正数或负数
C.正整数
D.以上全不对
答案:
D [解析]字母可以表示任何数,即a可以表示正数、0或负数,所以A,B,C三个选项都不全面.
3. 下列式子中,符合代数式书写格式的有(
①$m × n$;②$3\frac{1}{3}ab$;③$\frac{1}{4}(x + y)$;④$m + 2$;⑤$abc^3$。
A.2个
B.3个
C.4个
D.5个
B
)①$m × n$;②$3\frac{1}{3}ab$;③$\frac{1}{4}(x + y)$;④$m + 2$;⑤$abc^3$。
A.2个
B.3个
C.4个
D.5个
答案:
B [解析]①正确的书写格式是mn;②正确的书写格式是$\frac{10}{3}ab$;③④⑤的书写格式是正确的.
4. 在式子$n - 3$,$a^2b^3$,$m + s \lt 2$,$1 + 80\%t$,$-xy$,$S = ab$中,代数式有(
A.1个
B.2个
C.3个
D.4个
D
)A.1个
B.2个
C.3个
D.4个
答案:
D [解析]所给式子中,$m+s<2$含有小于号,不是代数式;$S=ab$中含有等号,不是代数式;$n-3$,$a^{2}b^{3}$,$1+80\%t$,$-xy$是代数式,因此代数式有4个.
5. 代数式$\frac{1}{a + b}$表示的意义是(
A.$a与b$的和
B.$a与b$的倒数和
C.$a与b$的倒数的和
D.$a与b$的和的倒数
D
)A.$a与b$的和
B.$a与b$的倒数和
C.$a与b$的倒数的和
D.$a与b$的和的倒数
答案:
D
6. 现有30个数,其中所有正数之和为10,负数之和为$a$,这30个数的绝对值之和为(
A.$10 + a$
B.$20 + a$
C.$10 - a$
D.$20 - a$
10-a
)A.$10 + a$
B.$20 + a$
C.$10 - a$
D.$20 - a$
答案:
C [解析]根据正数的绝对值等于其本身,负数的绝对值等于它的相反数,可得这30个数的绝对值之和为$10-a$.
7. 代入法 若$x = \frac{4}{3}$,则代数式$4 - 3x$的值为(
A.$-1$
B.0
C.1
D.2
0
)A.$-1$
B.0
C.1
D.2
答案:
B [解析]当$x=\frac{4}{3}$时,$4-3x=4-3×\frac{4}{3}=4-4=0$.
8. 应用意识 某校需完成一定的植树任务,其中九年级共种了任务数的一半,八年级种了剩下任务数的$\frac{2}{3}$,七年级共种了$a$棵树苗。则该校植树的任务数为(
A.$6a$
B.$5a$
C.$4a$
D.$3a$
6a
)A.$6a$
B.$5a$
C.$4a$
D.$3a$
答案:
A [解析]七年级种了a棵,占剩下一半的$\frac{1}{3}$,八年级种的占剩下一半的$\frac{2}{3}$,故八年级种了2a棵,一半就是3a棵,则九年级种了3a棵,故总任务是6a棵.
9. 规律探索 观察下面两行数:
$1$,$5$,$11$,$19$,$29$,…;
$1$,$3$,$6$,$10$,$15$,…。
取每行数的第7个数,计算这两个数的和是(
A.92
B.87
C.83
D.78
$1$,$5$,$11$,$19$,$29$,…;
$1$,$3$,$6$,$10$,$15$,…。
取每行数的第7个数,计算这两个数的和是(
83
)A.92
B.87
C.83
D.78
答案:
C [解析]观察第2行数可知,第7个数为$1+2+3+4+5+6+7=28$,第1行的第7个数为$28×2-1=55$,因为$28+55=83$,所以取每行数的第7个数,这两个数的和是83.
10. 流程图 按如图所示的运算程序,若输入的$x = -5$,则输出的结果为(
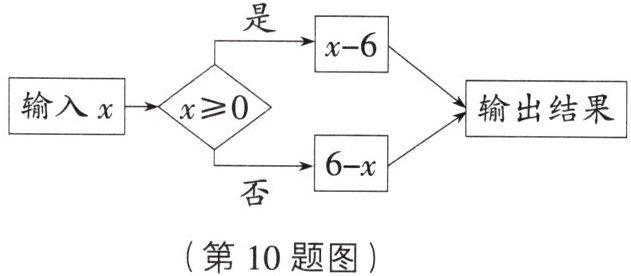
A.11
B.$-3$
C.$-1$
D.1
A
)
A.11
B.$-3$
C.$-1$
D.1
答案:
A [解析]因为$-5<0$,所以当$x=-5$时,$6-x=6-(-5)=6+5=11$.
11. 如图,数轴上四点$A$,$C$,$O$,$B$中,其中$O$为原点,且$AC = 3$,$OA = OB$,若点$C表示的数为x$,则点$B$表示的数为(
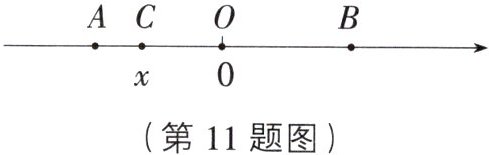
A.$-(x + 3)$
B.$-(x - 3)$
C.$x + 3$
D.$x - 3$
$-(x-3)$
)
A.$-(x + 3)$
B.$-(x - 3)$
C.$x + 3$
D.$x - 3$
答案:
B [解析]因为$AC=3$,点C表示的数为x,所以点A表示的数为$x-3$.又因为$OA=OB$,O为原点,所以点B表示的数为$-(x-3)$.
12. 新定义 $a$是不为2的有理数,我们把$\frac{2}{2 - a}称为a$的“哈利数”,如3的“哈利数”是$\frac{2}{2 - 3} = -2$,$-2$的“哈利数”是$\frac{2}{2 - (-2)} = \frac{1}{2}$。已知$a_1 = 3$,$a_2是a_1$的“哈利数”,$a_3是a_2$的“哈利数”,$a_4是a_3$的“哈利数”,……$$,依次类推,则$a_{2024}= $(
A.3
B.$-2$
C.$\frac{1}{2}$
D.$\frac{4}{3}$
$\frac{4}{3}$
)A.3
B.$-2$
C.$\frac{1}{2}$
D.$\frac{4}{3}$
答案:
D [解析]$a_{1}=3$,$a_{2}=\frac{2}{2-3}=-2$,$a_{3}=\frac{2}{2-(-2)}=\frac{1}{2}$,$a_{4}=\frac{2}{2-\frac{1}{2}}=\frac{4}{3}$,$a_{5}=\frac{2}{2-\frac{4}{3}}=3$,所以每4个数为一周期循环,因为$2024÷4=506$,所以$a_{2024}=a_{4}=\frac{4}{3}$.
查看更多完整答案,请扫码查看


