《2025年考点集训与满分备考七年级数学上册冀教版》

8. 应用意识 下列现象说明“点动成线”的是(B)
A.汽车雨刷在挡风玻璃上面画出的痕迹
B.扔一块小石子,石子在空中飞行的路线
C.旋转一扇门,门在空中运动的痕迹
D.电风扇通电后它的扇叶旋转,在空中形成的图形

答案： B ［解析］A现象属于“线动成面”;B现象属于“点动成线”;C现象属于“面动成体”;D现象属于“线动成面”.

9. 已知旋转前图形求几何体 将下列平面图形绕虚线旋转一周,可以得到如图所示的立体图形的是(A)

答案： A ［解析］题图所示的立体图形是由内凹,且上面长、下面短的平面图形绕虚线旋转一周得到的.

10. 如图所示的立体图形是由5个面围成的；面与面相交成9条线,其中有2条线是曲的。

答案： 5 9 2

11. 跨学科·语文 在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这种生活现象可以反映的数学原理是点动成线。

答案： 点动成线

12. 较难题 如图,已知直角三角形纸板ABC,直角边AB= 4cm,BC= 8cm。
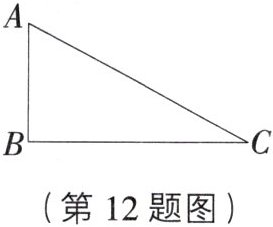
(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到3种大小不同的几何体；
(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积。
(圆锥的体积= $\frac{1}{3}\pi r^{2}h$,其中$\pi$取3)

以AB边所在直线为轴:$\frac{1}{3}×3×8^{2}×4=\frac{1}{3}×3×64×4=256(cm^{3})$;以BC边所在直线为轴:$\frac{1}{3}×3×4^{2}×8=\frac{1}{3}×3×16×8=128(cm^{3})$. 答:以AB边所在直线为轴得到的圆锥的体积是$256cm^{3}$,以BC边所在直线为轴得到的圆锥的体积是$128cm^{3}$.

答案： ［解析］
(1)3
(2)以AB边所在直线为轴:$\frac{1}{3}×3×8^{2}×4=\frac{1}{3}×3×64×4=256(cm^{3})$;以BC边所在直线为轴:$\frac{1}{3}×3×4^{2}×8=\frac{1}{3}×3×16×8=128(cm^{3})$. 答:以AB边所在直线为轴得到的圆锥的体积是$256cm^{3}$,以BC边所在直线为轴得到的圆锥的体积是$128cm^{3}$. 归纳总结 在判断由平面图形旋转成的立体图形的形状时,要弄清两点:一是进行旋转的平面图形的形状;二是平面图形绕着哪条直线进行旋转.分析时不要漏情况,如将一个直角三角形绕一边所在直线旋转可以得出三种情况.

13. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征。
甲同学：它有4个面,每个面都是三角形。
乙同学：它有6条棱。
则该模型对应的立体图形可能是(C)
A.三棱柱
B.四棱柱
C.三棱锥
D.四棱锥

答案： C ［解析］侧面是三角形,说明它是棱锥,底面是三角形,说明它是三棱锥.

14. 中考新考法方案选择 小明想通过绕轴旋转某平面图形得到如图1所示的圆柱(数据如图所示),他和同学们想到了以下方案：
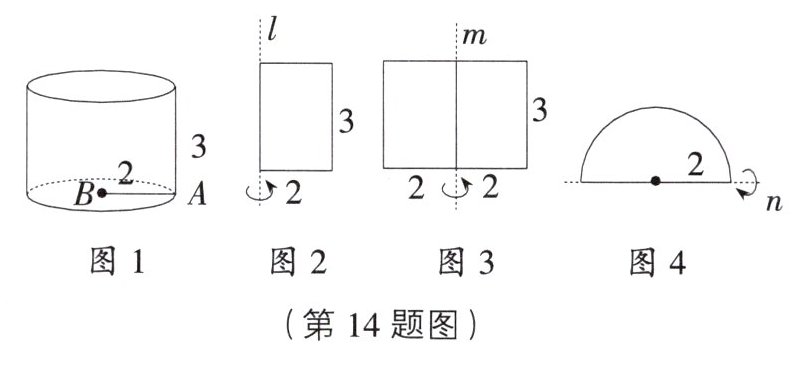
小明：如图2,将长为3、宽为2的长方形绕直线l旋转一周可以得到。
小亮：如图3,将长为4、宽为3的长方形绕直线m旋转半周可以得到。
小红：如图4,将半径为2的半圆绕直线n旋转一周可以得到。
请问谁的方案正确？并将不正确的方案旋转后得到的图形写出来。

答案： ［解析］小明和小亮的方案正确；将半径为2的半圆绕直线n旋转一周得到球,所以小红的方案不正确.