第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
11. (1)图中可以用一个大写字母表示的角有
(2)以 $A$ 为顶点的角有
(3)图中一共有
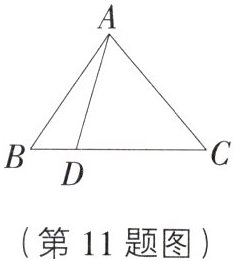
∠B,∠C
;(2)以 $A$ 为顶点的角有
∠BAD,∠DAC,∠BAC
;(3)图中一共有
7
个角(不包括平角).
答案:
(1)∠B,∠C
(2)∠BAD,∠DAC,∠BAC
(3)7 [解析]图中的角有∠B,∠C,∠BAD,∠DAC,∠BAC,∠BDA,∠ADC,共7个.
(1)∠B,∠C
(2)∠BAD,∠DAC,∠BAC
(3)7 [解析]图中的角有∠B,∠C,∠BAD,∠DAC,∠BAC,∠BDA,∠ADC,共7个.
12. (1) $37° 36'' = $
(2) $15° 24' 36'' = $
(3)把 $91.48°$ 化成度、分、秒的形式为
(4)把 $35.16°$ 化成度、分、秒的形式为
37.01
$°$;(2) $15° 24' 36'' = $
15.41
$°$;(3)把 $91.48°$ 化成度、分、秒的形式为
91°28'48''
;(4)把 $35.16°$ 化成度、分、秒的形式为
35°9'36''
.
答案:
(1)37.01
(2)15.41
(3)91°28'48''
(4)35°9'36'' [解析]
(1)37°36'=37°+$(\frac{36}{60})^{\circ}$=37°+0.6'=37°+$(\frac{0.6}{60})^{\circ}$=37°+0.01°=37.01°;
(2)15°24'36''=15°24'+$(\frac{36}{60})'$=15°24'+0.6'=15°24.6'=15°+$(\frac{24.6}{60})^{\circ}$=15°+0.41°=15.41°;
(3)91.48°=91°28.8'=91°28'48'';
(4)35.16°=35°+60'×0.16=35°9'+60''×0.6=35°9'36''.
(1)37.01
(2)15.41
(3)91°28'48''
(4)35°9'36'' [解析]
(1)37°36'=37°+$(\frac{36}{60})^{\circ}$=37°+0.6'=37°+$(\frac{0.6}{60})^{\circ}$=37°+0.01°=37.01°;
(2)15°24'36''=15°24'+$(\frac{36}{60})'$=15°24'+0.6'=15°24.6'=15°+$(\frac{24.6}{60})^{\circ}$=15°+0.41°=15.41°;
(3)91.48°=91°28.8'=91°28'48'';
(4)35.16°=35°+60'×0.16=35°9'+60''×0.6=35°9'36''.
13. 如图所示.
(1) $∠1$ 表示成 $∠A$, $∠2$ 表示成 $∠D$, $∠3$ 表示成 $∠C$,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?

(1) $∠1$ 表示成 $∠A$, $∠2$ 表示成 $∠D$, $∠3$ 表示成 $∠C$,这样的表示方法对不对?如果不对,应该怎样改正?
(2)图中哪个角可以用一个字母来表示?
(3)图中共有几个小于平角的角?

答案:
[解析]
(1)不对.改正:∠1表示成∠DAC;∠2表示成∠ADC;∠3表示成∠ECF;
(2)图中∠B可以用一个字母表示;
(3)图中小于平角的角有11个,分别为∠BAD,∠1,∠BAC,∠B,∠ADB,∠2,∠ACD,∠ACE,∠3,∠ECD,∠ACF.
(1)不对.改正:∠1表示成∠DAC;∠2表示成∠ADC;∠3表示成∠ECF;
(2)图中∠B可以用一个字母表示;
(3)图中小于平角的角有11个,分别为∠BAD,∠1,∠BAC,∠B,∠ADB,∠2,∠ACD,∠ACE,∠3,∠ECD,∠ACF.
14. 如图,用量角器测得 $∠ABC$ 的度数是(
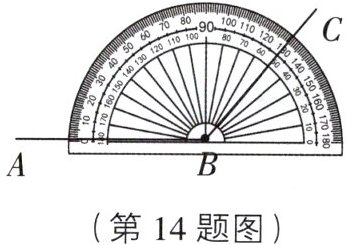
A.$50°$
B.$80°$
C.$130°$
D.$150°$
C
)
A.$50°$
B.$80°$
C.$130°$
D.$150°$
答案:
C
15. $74° 19' 30'' = $
74.325
$°$.
答案:
74.325 [解析]30×$(\frac{1}{60})'$=0.5',19'+0.5'=19.5',19.5×$(\frac{1}{60})^{\circ}$=0.325°,74°+0.325°=74.325°.
16. 中考新考法 规律探究 如图,观察图形,回答下列问题.
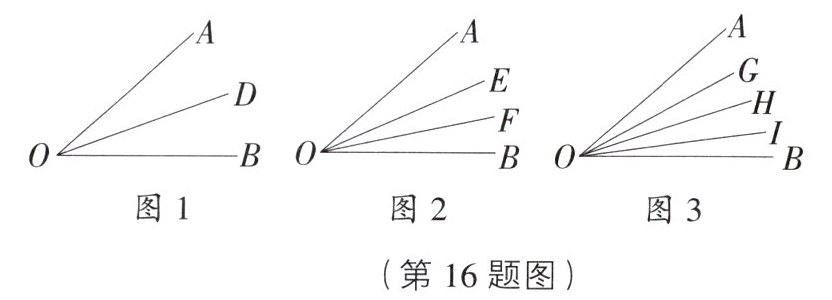
(1)如图 1,在 $∠AOB$ 内以 $O$ 为端点画 1 条射线,此时图中有多少个角?
(2)如图 2,在 $∠AOB$ 内以 $O$ 为端点画 2 条射线,此时图中有多少个角?
(3)如图 3,在 $∠AOB$ 内以 $O$ 为端点画 3 条射线,此时图中有多少个角?
(4)若在 $∠AOB$ 内以 $O$ 为端点画 10 条射线,图中有多少个角?画 $n$ 条射线呢?

(1)如图 1,在 $∠AOB$ 内以 $O$ 为端点画 1 条射线,此时图中有多少个角?
(2)如图 2,在 $∠AOB$ 内以 $O$ 为端点画 2 条射线,此时图中有多少个角?
(3)如图 3,在 $∠AOB$ 内以 $O$ 为端点画 3 条射线,此时图中有多少个角?
(4)若在 $∠AOB$ 内以 $O$ 为端点画 10 条射线,图中有多少个角?画 $n$ 条射线呢?
答案:
[解析]
(1)此时图中有3条射线,角的个数为$\frac{3×(3-1)}{2}$=3(个);
(2)此时图中有4条射线,角的个数为$\frac{4×(4-1)}{2}$=6(个);
(3)此时图中有5条射线,角的个数为$\frac{5×(5-1)}{2}$=10(个);
(4)若在∠AOB内画10条射线,此时图中有12条射线,角的个数为$\frac{12×(12-1)}{2}$=66(个),画n条射线,图中共有(n+2)条射线,所以共有$\frac{(n+2)(n+1)}{2}$个角.
(1)此时图中有3条射线,角的个数为$\frac{3×(3-1)}{2}$=3(个);
(2)此时图中有4条射线,角的个数为$\frac{4×(4-1)}{2}$=6(个);
(3)此时图中有5条射线,角的个数为$\frac{5×(5-1)}{2}$=10(个);
(4)若在∠AOB内画10条射线,此时图中有12条射线,角的个数为$\frac{12×(12-1)}{2}$=66(个),画n条射线,图中共有(n+2)条射线,所以共有$\frac{(n+2)(n+1)}{2}$个角.
查看更多完整答案,请扫码查看


