《2025年考点集训与满分备考七年级数学上册冀教版》

1. 如图,下列关系式与图不符合的是(C)

A.$AD - CD = AB + BC$
B.$AC - BC = AD - BD$
C.$AC - BC = AC + BD$
D.$AD - AC = BD - BC$

答案： C [解析] A.AD - CD = AB + BC,正确,B.AC - BC = AD - BD,正确;C.AC - BC = AB,而AC + BD ≠ AB,故本选项错误;D.AD - AC = BD - BC,正确.

2. 如图,已知线段$a$,$b$,请画一条线段,使它的长度等于$a - 2b$。

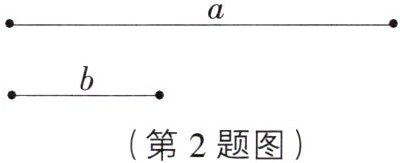
答案：
[解析] 如图，线段 AE 即所求.

方法归纳
画两条线段的差→画较长的线段→在其上画出较短的线段(其中一个端点重合)→不重合的部分即两条线段的差.

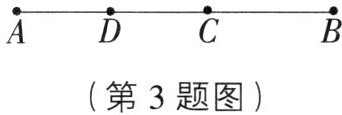
3. 如图,$CB = 4\ cm$,$DB = 7\ cm$,$D为AC$的中点,则$AB$的长为(D)

A.$7\ cm$
B.$8\ cm$
C.$9\ cm$
D.$10\ cm$

答案： D [解析] 由题意知,CB = 4cm,DB = 7cm,所以 DC = 3cm.又因为 D 为 AC 的中点,所以 AD = DC = 3cm,故 AB = AD + DB = 3 + 7 = 10(cm).

4. 如图,长为$12\ cm的线段AB的中点为M$,点$C将线段MB分成MC:CB = 1:2$,则线段$AC$的长度为8 $cm$。

答案： 8 [解析] 因为线段 AB 的中点为 M,所以 AM = MB = 6cm.
因为 MC:CB = 1:2,MC + CB = MB,所以 MC = $\frac{1}{1 + 2}$MB = 2cm.
所以 AC = AM + MC = 6 + 2 = 8(cm).

5. 已知线段$AB = 8\ cm$,在直线$AB上画线段BC$,使它等于$3\ cm$,则线段$AC$等于( )

A.$11\ cm$
B.$5\ cm$
C.$11\ cm或5\ cm$
D.$8\ cm或11\ cm$

答案：
C [解析] 由于点 C 的位置不确定,故要分两种情况讨论:
(1)如图 1,当点 C 在点 B 右侧时,AC = AB + BC = 8 + 3 = 11(cm);

(2)如图 2,当点 C 在点 B 左侧时,AC = AB - BC = 8 - 3 = 5(cm).

所以线段 AC 等于 5cm 或 11cm.
易错分析
当题目条件中没有图形,或有些条件的表述不明确时,通常要用到分类讨论思想,对不明确地方的几种可能性进行分析.

6. 一支水笔正好与一把直尺平靠放在一起,小明发现：水笔的笔尖端($A$点)正好对着直尺刻度约为$5.6\ cm$处,另一端($B$点)正好对着直尺刻度约为$20.6\ cm$处。则水笔的中点位置的刻度约为(13.1cm)
A.$15\ cm$
B.$7.5\ cm$
C.$13.1\ cm$
D.$12.1\ cm$

答案： C [解析] 因为水笔的笔尖端(A 点)正好对着直尺刻度约为 5.6cm 处,另一端(B 点)正好对着直尺刻度约为 20.6cm 处.所以水笔的长度为 20.6 - 5.6 = 15(cm),水笔的一半为 15÷2 = 7.5(cm),所以水笔的中点位置的刻度约为 5.6 + 7.5 = 13.1(cm).

7. 如图,线段$AB = 12\ cm$,$C是线段AB$上任意一点,$M$,$N分别是AC$,$BC$的中点,$MN$的长为6 $cm$,如果$AM = 4\ cm$,那么$BN$的长为2 $cm$。

答案： 6 2 [解析] 由题意知,MN = $\frac{1}{2}$AB = $\frac{1}{2}$×12 = 6(cm),AM = 4cm,则 BM = AB - AM = 12 - 4 = 8(cm),BN = BM - MN = 8 - 6 = 2(cm).

8. 如图,$C是线段AB$上一点,$M是AC$的中点,$N是BC$的中点。若$AM = 1$,$BC = 4$,则$MN$的长度为3。

答案： 3 [解析] 因为 M 是 AC 的中点,N 是 BC 的中点,AM = 1,BC = 4,所以 CN = 2,AM = CM = 1,所以 MN = MC + CN = 3.

9. 如图,已知线段$a$,$b$,求作线段$AB$,使得$AB = 3a - 2b$。

答案：
[解析] 如图，线段 AB 即所求.