《2025年考点集训与满分备考七年级数学上册冀教版》

12. 化简：$3x^{2} - \left[5x - \left(\dfrac{1}{2}x - 3\right) + 2x^{2}\right]$。

答案： ［解析］解法一:(由内向外逐层去括号)3x²-[5x-($\frac{1}{2}$x-3)+2x²]=3x²-(5x-$\frac{1}{2}$x+3+2x²)=3x²-5x+$\frac{1}{2}$x-3-2x²=x²-$\frac{9}{2}$x-3;解法二:(由外向内逐层去括号)3x²-[5x-($\frac{1}{2}$x-3)+2x²]=3x²-5x+($\frac{1}{2}$x-3)-2x²=3x²-5x+$\frac{1}{2}$x-3-2x²=x²-$\frac{9}{2}$x-3;解法三:(由内向外逐层去括号,且边去括号边合并)3x²-[5x-($\frac{1}{2}$x-3)+2x²]=3x²-(5x-$\frac{1}{2}$x+3+2x²)=3x²-($\frac{9}{2}$x+3+2x²)=3x²-$\frac{9}{2}$x-3-2x²=x²-$\frac{9}{2}$x-3. 解题通法 含多层括号,可按由内到外依次去掉括号,也可以由外到内依次去掉括号;可去完括号后再合并,也可以边去括号边合并.

13. 先化简,再求值：
$2xy + \dfrac{1}{3}(3xy - 8y^{2}) - 6\left(\dfrac{2}{3}xy - y^{2}\right)$,其中$x = -1$,$y = 3$。

答案： ［解析］原式=2xy+xy-$\frac{8}{3}$y²-4xy+6y²=-xy+$\frac{10}{3}$y²,当x=-1,y=3时,原式=-(-1)×3+$\frac{10}{3}$×3²=3+30=33.

14. 以下是小明同学化简代数式的过程。
$\begin{array}{l}(a^{2}b + 4ab) - 3(ab - a^{2}b)\\= a^{2}b + 4ab - 3ab - 3a^{2}b …………………\quad 第一步\\= a^{2}b - 3a^{2}b + 4ab - 3ab …………………\quad 第二步\\= ab - 2a^{2}b. ………………………………\quad 第三步\end{array} $
(1)小明同学的解答过程在第一步开始出错,出错原因是去掉括号时,-a²b没有变号；
(2)小明同学在解答的过程中用到了去括号法则,去括号的依据是乘法对加法的分配律；
(3)请你帮助小明同学写出正确的解答过程。
(a²b+4ab)-3(ab-a²b)=a²b+4ab-3ab+3a²b=4a²b+ab.

答案：
(1)一 去掉括号时,-a²b没有变号
(2)乘法对加法的分配律
(3)(a²b+4ab)-3(ab-a²b)=a²b+4ab-3ab+3a²b=4a²b+ab.

15. “$\otimes$”表示一种运算符号,其定义是$a\otimes b = -2a + b$。如$3\otimes 7 = -2× 3 + 7$。
(1)$x\otimes (-5) = $-2x-5；
(2)若$x = -1$,化简多项式$3x^{2} - x^{3} - (6x^{2} - 7x) - 2(x^{3} - 3x^{2} - 4x)$,并求出它的值。
原式=3x²-x³-6x²+7x-2x³+6x²+8x=-3x³+3x²+15x,当x=-1时,原式=-3×(-1)³+3×(-1)²+15×(-1)=-3×(-1)+3×1-15=3+3-15=-9.

答案：
(1)-2x-5
(2)原式=3x²-x³-6x²+7x-2x³+6x²+8x=-3x³+3x²+15x,当x=-1时,原式=-3×(-1)³+3×(-1)²+15×(-1)=-3×(-1)+3×1-15=3+3-15=-9.

16. 王明在准备化简代数式$3(3x^{2} + 4xy) - ■(2x^{2} + 3xy - 1)$时不小心将墨水滴在了作业本上,使得$(2x^{2} + 3xy - 1)$前面的系数看不清了,于是王明就询问老师,老师为了测试王明对知识的掌握程度,于是对王明说：“该题标准答案的结果不含有$y$。”请你通过老师的话语,帮王明解决如下问题：
(1)■的值为4；
(2)求出该题的标准答案。
$3(3x^{2} + 4xy) - 4(2x^{2} + 3xy - 1)=9x^{2} + 12xy - 8x^{2} - 12xy + 4=x^{2} + 4$

答案：
(1)4 提示:设■的值为a.则3(3x²+4xy)-a(2x²+3xy-1)=9x²+12xy-2ax²-3axy+a=(9-2a)x²+(12-3a)xy+a.由于结果不含有y,所以12-3a=0,解得a=4;
(2)3(3x²+4xy)-4(2x²+3xy-1)=9x²+12xy-8x²-12xy+4=x²+4.

17. 如图,大正方形的边长为$a$,小正方形的边长为$2$,求阴影部分的面积。

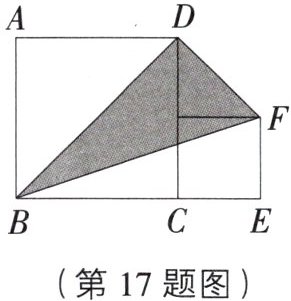
答案： ［解析］S阴影=S梯形FECD+S三角形BCD-S三角形BEF=$\frac{1}{2}$(a+2)×2+$\frac{1}{2}$×a×a-$\frac{1}{2}$(a+2)×2=$\frac{1}{2}$a².

18. 计算：$2a^{2} - (a^{2} + 2) = $$a^{2}-2$。

答案： a²-2

19. 观察下列各式：①$-a + b = -(a - b)$；②$2 - 3x = -(3x - 2)$；③$5x + 30 = 5(x + 6)$；④$-x - 6 = -(x + 6)$。探索以上四个式子中括号的变化情况,思考它和去括号法则的异同。利用你探索出来的规律,解答下面的题目：
已知$a^{2} + b^{2} = 5$,$1 - b = -2$,求$-1 + a^{2} + b + b^{2}$的值。

答案： ［解析］因为a²+b²=5,1-b=-2,所以-1+a²+b²=-(1-b)+(a²+b²)=-(-2)+5=7.