《2025年考点集训与满分备考七年级数学上册冀教版》

10. 较难题 如图，线段 AB 表示一条对折以后的绳子，现从 P 处把绳子剪断，剪断后的各段绳子中最长的一段为 32 cm. 若 AP = $\frac{1}{2}$PB，则这条绳子的原长为（48cm 或 96cm）

A.48 cm
B.96 cm
C.48 cm 或 96 cm
D.64 cm 或 96 cm

答案： C ［解析］分两种情况讨论：①当 PB 的 2 倍最长时，由题意得，PB=$\frac{1}{2}$×32=16(cm)，所以 AP=$\frac{1}{2}$PB=8(cm)，所以 AB=AP + PB=24(cm)，所以这条绳子的原长为 2AB=48cm；②当 AP 的 2 倍最长时，由题意得，AP=$\frac{1}{2}$×32=16(cm)，因为 AP=$\frac{1}{2}$PB，所以 PB=2AP=32cm，所以 AB=AP + PB=48cm，所以这条绳子的原长为 2AB=96cm.综上可知，这条绳子的原长为 48cm 或 96cm.

11. 优秀传统文化 “齐天大圣”孙悟空有一个宝贝——金箍棒，当他快速旋转金箍棒时，展现在我们眼前的是一个圆的形象，这说明线动成面.

答案： 线动成面

12. 如图，直线上四点 A，B，C，D，看图填空：①AC =AB + BC；②CD = AD -AC；③AC + BD - BC =AD.

答案： AB AC AD

13. 新定义 已知 A，B，C 是同一条数轴上的三个点，点 A 在数轴上表示的数是 1，AB = 2，当点 B 在点 A 右侧时，若 A，B，C 有一点是另一条线段的中点，则点 A，B，C 称为“和谐点”，点 C 在数轴上表示的数是-1 或 2 或 5.

答案： -1 或 2 或 5 ［解析］①当 A 为 CB 中点时，因为 AB=2，所以 CA=AB=2，又因为点 A 在数轴上表示的数是 1，所以 C 在数轴上表示的数为 1 - CA=1 - 2=-1；②当 B 为 AC 中点时，因为 AB=2，所以 BC=AB=2，又因为点 A 在数轴上表示的数是 1，所以点 C 在数轴上表示的数为 1 + AB + BC=1 + 2 + 2=5；③当 C 为 AB 中点时，因为 AB=2，所以 AC=CB=$\frac{1}{2}$AB=1，又因为点 A 在数轴上表示的数是 1，所以点 C 在数轴上表示的数为 1 + AC=1 + 1=2.综上所述，点 C 在数轴上表示的数是 -1 或 2 或 5.

14. （12 分）分类讨论法 如图，点 C 为线段 AD 上一点，点 B 为 CD 的中点，且 AD = 13 cm，BC = 3 cm.
（1）图中共有多少条线段？请写出这些线段.
（2）求 AC 的长.
（3）若点 E 在直线 AD 上，且 EA = 4 cm，求 BE 的长.

答案：

(1)图中的线段有 AC,AB,AD,CB,CD,BD，共 6 条；
(2)因为 B 为 CD 的中点，BC=3cm，所以 CD=2BC=6cm，因为 AD=13cm，所以 AC=AD - CD=7cm；
(3)如图 1，当点 E 在线段 AC 上时，因为 AB=AC + BC=10cm，EA=4cm，所以 BE=AB - EA=10 - 4=6(cm)；如图 2，当点 E 在 CA 延长线上时， 因为 AB=10cm，EA=4cm，所以 BE=EA + AB=14cm.综上所述，BE 的长为 6cm 或 14cm.

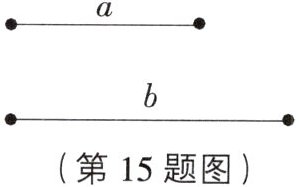
15. （14 分）已知线段 a，b（如图），根据下列要求，依次画图并计算.
（1）画出一条线段 OA，使它等于 3a - b.
（2）若 a = 2，b = 3，M 是线段 OA 的中点，求线段 OM 和线段 MD 的长.

答案：

(1)如图，线段 OA 即所求；

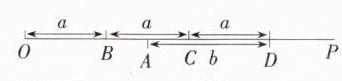
(2)因为 a=2，b=3，所以 OA=3a - b=3.因为 M 是线段 OA 的中点，所以 OM=$\frac{1}{2}$OA=$\frac{3}{2}$.因为 OB=BC=CD=a，所以 OD=OB + BC + CD=3a=6.所以 MD=OD - OM=6 - $\frac{3}{2}$=$\frac{9}{2}$.

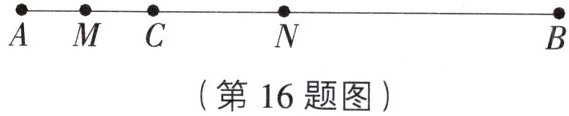
16. （16 分）如图，线段 AB = 20，BC = 15，M 是 AC 的中点，在 CB 上取一点 N，使得 CN：NB = 2:3.求线段 MN 的长.

答案： ［解析］因为 AB=20，BC=15，CN:NB=2:3，所以 CN=$\frac{2}{5}$BC=$\frac{2}{5}$×15=6，AC=AB - BC=20 - 15=5.又因为 M 是 AC 的中点，所以 MC=$\frac{1}{2}$AC=$\frac{5}{2}$，所以 MN=MC + CN=$\frac{17}{2}$，即线段 MN 的长是$\frac{17}{2}$.

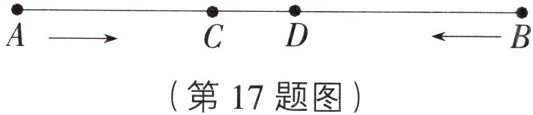
17. （16 分）如图，甲、乙两车分别自 A，B 两地同时出发（匀速），相向而行，在 C 地相遇后，继续行驶分别到达 B，A 两地后立即返回，在 D 处第二次相遇，若 AC = 60 km，两相遇地相距 10 km，则到第二次相遇时，乙车比甲车多行驶多少千米？

答案： ［解析］第一次相遇时，甲车行了 60km，从第一次相遇到第二次相遇，两车路程之和为 2AB，是第一次相遇时所走路程之和的 2 倍，故从第一次相遇到第二次相遇，甲车走了 60×2=120(km)，则 BD + BC=2BD + CD=120(km)，因为两相遇地相距 10km，所以 CD=10km，所以 BD=55km，因为 AD=AC + CD=60 + 10=70(km)，所以到第二次相遇乙车比甲车多行（AB + AD）-（AB + BD）=AD - BD=70 - 55=15(km).答：到第二次相遇时，乙车比甲车多行 15km.