《2025年拔尖特训七年级数学上册人教版》

5. (2024·北京二模)如图,七年级准备制作一条长为8.5m的横幅,横幅内容定为16个字,对横幅的有关数据作如下规定:每个字的字宽是相同的,每两个字之间的字距均相等,边空宽:字宽:字距= 3:4:1,则横幅的字距是0.1m.

答案： 0.1 解析:设横幅的字距是x m,则字宽是4x m,边空宽是3x m.根据题意,得2×3x+16×4x+(16-1)x=8.5,解得x=0.1.所以横幅的字距是0.1 m.

6. 已知关于x的方程3(x-2)= x-a的解比方程$\frac{x+a}{2}= \frac{2x-a}{3}的解小\frac{5}{2},$求a的值.

答案： 解方程3(x-2)=x-a,得x=$\frac{6-a}{2}$.解方程$\frac{x+a}{2}$=$\frac{2x-a}{3}$,得x=5a.根据题意,得$\frac{6-a}{2}$=5a-$\frac{5}{2}$,解得a=1.

7. (2025·呼伦贝尔扎兰屯期末)小明家经营一家文化创意产品商店,他在课余时间关注了文化创意背包和文化创意摆件两种商品的销售情况,如下表:

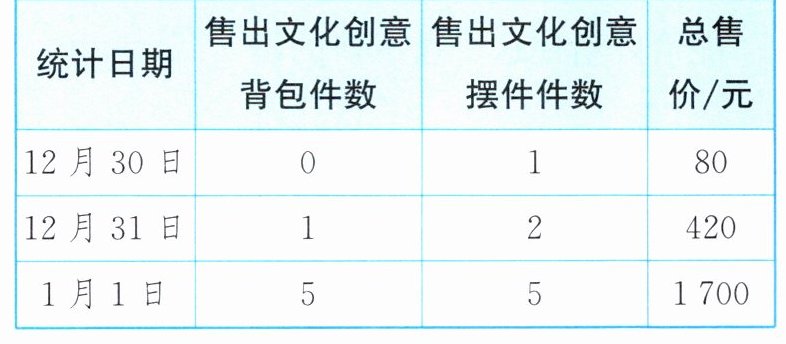
若小明家的文化创意产品商店售出文化创意背包和文化创意摆件共15件,总售价为3000元,则售出文化创意背包和文化创意摆件各多少件?

答案： 由题意可知,售出1件文化创意摆件的价格为80元,售出1件文化创意背包的价格为420-2×80=260(元).设售出文化创意背包x件,则售出文化创意摆件(15-x)件.由题意,得260x+80(15-x)=3000,解得x=10.所以15-x=15-10=5.所以售出文化创意背包10件,售出文化创意摆件5件.

8. (2025·泰州兴化期末)阅读理解:勤奋好学的小丽发明了降次小魔方(如图),利用该魔方可以将二次多项式降次为一次多项式.规则如下:将二次多项式M的二次项指数与二次项系数相乘,其积作为一次多项式N的一次项系数,二次多项式M的一次项系数作为一次多项式N的常数项,二次多项式M的常数项变为0.如,二次多项式M= 3x²+4x+1经过降次小魔方后,可以降次为一次多项式N= 6x+4.
理解应用:
(1)若A= 6x²-2x+5,则经过降次小魔方后得到的多项式B= ______12x-2.
(2)已知A= 4x²+3(x-6),经过降次小魔方后得到的多项式记为B.若A-mB的结果中不含一次项,求常数m的值.
根据降次小魔方的规则,得B=8x+3,所以A-mB=4x²+3(x-6)-m(8x+3)=4x²+(3-8m)x-(18+3m).因为A-mB的结果中不含一次项,所以3-8m=0,解得m=$\frac{3}{8}$.
(3)已知A= (a-2)x²-(4+b)x+1(a,b为常数),经过降次小魔方后得到的多项式记为B.若方程B= 3x+5b有无数个解,分别求a,b的值.
根据降次小魔方的规则,得B=2(a-2)x-(4+b).因为B=3x+5b,所以2(a-2)x-(4+b)=3x+5b.整理,得(2a-7)x=6b+4.又因为方程B=3x+5b有无数个解,所以方程(2a-7)x=6b+4有无数个解.所以2a-7=0且6b+4=0.所以a=$\frac{7}{2}$,b=-$\frac{2}{3}$.

答案：
(1)12x-2.
(2)根据降次小魔方的规则,得B=8x+3,所以A-mB=4x²+3(x-6)-m(8x+3)=4x²+(3-8m)x-(18+3m).因为A-mB的结果中不含一次项,所以3-8m=0,解得m=$\frac{3}{8}$.
(3)根据降次小魔方的规则,得B=2(a-2)x-(4+b).因为B=3x+5b,所以2(a-2)x-(4+b)=3x+5b.整理,得(2a-7)x=6b+4.又因为方程B=3x+5b有无数个解,所以方程(2a-7)x=6b+4有无数个解.所以2a-7=0且6b+4=0.所以a=$\frac{7}{2}$,b=-$\frac{2}{3}$.