《2025年拔尖特训七年级数学上册人教版》

1. 当$x= -1,y= 3$时,代数式$x^{3}-2y$的值为(A)
A.-7
B.-5
C.4
D.7

答案： A

2. 若$(2m+1)^{2}+2|n-3|= 0$,则代数式$m^{n}$的值是(B)
A.$-\frac{1}{6}$
B.$-\frac{1}{8}$
C.$\frac{1}{4}$
D.8

答案： B

3. 如果$x+2y= 5$,那么$3x+6y-1$的值是14.

答案： 14

4. 同一温度下,华氏温度$y(^{\circ}F)与摄氏温度x(^{\circ}C)之间的关系是y= \frac{9}{5}x+32$.如果某一温度下,摄氏温度是$40^{\circ}C$,那么华氏温度是104$^{\circ}F$.

答案： 104

5. (2025·揭阳揭西期末改编)对于两个有理数$m,n$,定义一种新的运算“*”:$m*n= 2m-3n$.根据以上规定解答下列各题:
(1) 求$4*(-3)$的值.
(2) 若$a= 3,b= -1$,求$a^{2}*b^{2}$的值.

答案： （1）4*(-3)=2×4-3×(-3)=17.（2）a²*b²=2a²-3b²=2×3²-3×(-1)²=18-3=15.

6. (2024·南京期末)关于代数式$1-m^{2}$的值,下列说法中一定正确的是(D)
A.比1小
B.比-1大
C.比$m^{2}$小
D.比$-m^{2}$大

答案： D

7. (2025·镇江句容期末)若当$x= 1$时,$mx^{3}-nx+1$的值为4,则当$x= -1$时,$mx^{3}-nx+7$的值为(A)
A.4
B.5
C.6
D.7

答案： A 解析：由题意可知，m-n+1=4，所以m-n=3.所以当x=-1时，mx³-nx+7=-m+n+7=-(m-n)+7=-3+7=4.

8. (2024·德州期末)设$(x-1)^{3}= ax^{3}+bx^{2}+cx+d$,则$a-b+c-d$的值为(B)
A.2
B.8
C.-2
D.-8

答案： B 解析：因为当x=-1时，(-1-1)³=-a+b-c+d，所以-a+b-c+d=-8.所以a-b+c-d=8.

9. 已知当$x= a$时,代数式$-x+m与代数式x+n$的值都为8,则代数式$m+n= $16.

答案： 16 解析：因为当x=a时，代数式-x+m与代数式x+n的值都为8，所以-a+m=8，a+n=8.所以m=8+a，n=8-a.所以m+n=8+a+8-a=16.

10. 定义:若$a-b= 0$,则称$a与b$互为“代换数”.若$3x^{2}-5与-x+4$互为“代换数”,则代数式$6x^{2}+2x-5= $13.

答案： 13 解析：因为3x²-5与-x+4互为“代换数”，所以3x²-5-(-x+4)=0.所以3x²+x=9.所以6x²+2x-5=2(3x²+x)-5=2×9-5=13.

11. 火车站、机场等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为$a$cm,$b$cm,30 cm 的箱子(其中$a＞b$),准备采用如图①②所示的两种打包方式,所用打包带的总长(不计接头处的长)分别记为$l_{1},l_{2}$.

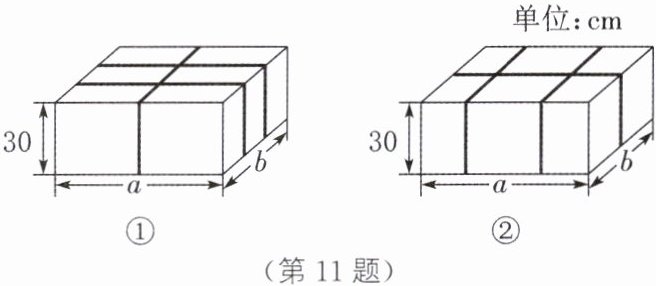
(1) 求图①中打包带的总长$l_{1}$、图②中打包带的总长$l_{2}$分别是多少(用含$a,b$的代数式表示).
(2) 当$a= 70,b= 50$时,计算两种打包方式所用的打包带总长各是多少,并判断哪一种打包方式更节省打包带.

答案： （1）题图①中打包带的总长l₁是4a+2b+30×6=(4a+2b+180)cm.题图②中打包带的总长l₂是2a+4b+30×6=(2a+4b+180)cm.（2）当a=70，b=50时，题图①中打包带的总长l₁是4×70+2×50+180=560(cm)，题图②中打包带的总长l₂是2×70+4×50+180=520(cm).因为560＞520，所以第二种打包方式更节省打包带.