《2025年拔尖特训七年级数学上册人教版》

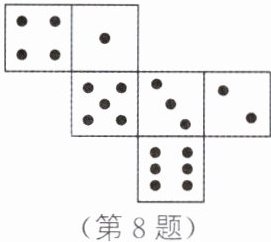
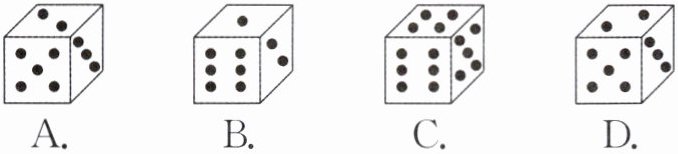
8. ★(2024·邢台期末)如图所示为一个正方体的展开图,则该正方体可能是 (C)

答案： C 解析：由正方体的展开图可知，点数2和5在相对面上，点数1和6在相对面上，所以选项A,B,D均不符合题意，选项C符合题意.
方法归纳
确定带标志的正方体的展开图的要点
一要掌握正方体的展开图的几种形状；二要注意相邻各面和相对各面的图案形状；三要综合各方面的条件加以判断.另外，根据展开图与立体图形的关系，可采用把展开图折叠为立体图形与已知的立体图形进行对比的方法来判断.

9.(2025·西安蓝田期末)如图所示为由若干个相同的小正方体搭成的几何体从前面、左面和上面看到的形状图,则搭成这个几何体的小正方体的个数是 ( )



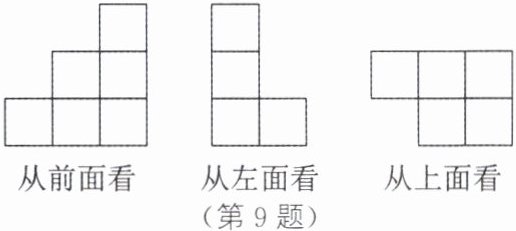
A.8
B.7
C.6
D.5

答案：
A 解析：因为从上面看到的形状图中有5个正方形，所以最底层有5个小正方体.综合从前面、左面看到的形状图，将各位置上的小正方体的个数标在从上面看到的形状图上（如图），则搭成这个几何体的小正方体的个数是1+1+1+2+3=8.

10.(2025·成都简阳期末)一个几何体由几个相同的小立方块搭成,从它的前面和上面看到的形状图如图所示.若搭成这个几何体最多需要a个小立方块,最少需要b个小立方块,则a+b= ______.

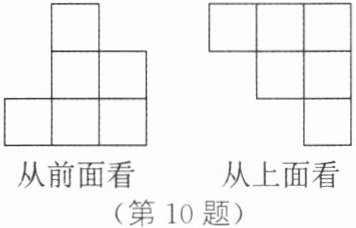
答案：
22 解析：如图，将各位置上的小立方块的个数标在从上面看到的形状图上，则a=1+3+3+2+2+2=13，b=1+1+1+1+2+3=9，所以a+b=13+9=22.

11.(2025·福州仓山期末)如图①所示为形状是长方体的某种包装盒,其中长：宽：高= 6：4：3,展开图如图②所示(不包含包装盒的黏合处).
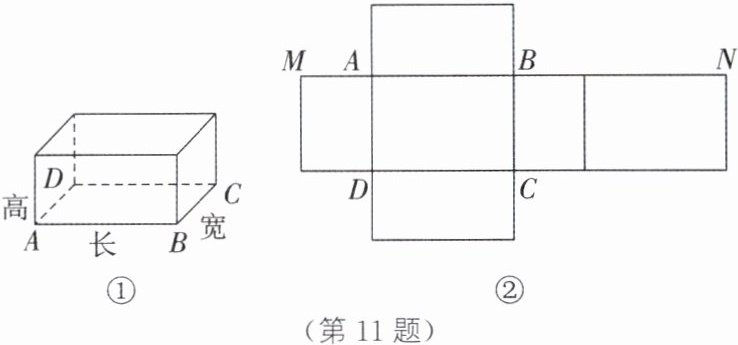
(1)设该包装盒的长为6x分米,则展开图中MN的长为______18x分米(用含x的代数式表示).
(2)若MN的长为18分米,现对包装盒外表面涂色(含底面),且每平方分米涂料的价格为0.25元,求整个包装盒外表面涂色的费用.因为MN的长为18分米，所以由（1），得18x=18，解得x=1.所以包装盒的长为6分米，宽为4分米，高为3分米.所以包装盒的表面积为2×(6×4+6×3+4×3)=108(平方分米).因为每平方分米涂料的价格为0.25元，所以整个包装盒外表面涂色的费用是0.25×108=27(元).

答案： （1）18x. 解析：因为包装盒的长为6x分米，长：宽：高=6:4:3，所以包装盒的宽为4x分米，高为3x分米.所以MN=2×3x+2×6x=18x(分米).
（2）因为MN的长为18分米，所以由（1），得18x=18，解得x=1.所以包装盒的长为6分米，宽为4分米，高为3分米.所以包装盒的表面积为2×(6×4+6×3+4×3)=108(平方分米).因为每平方分米涂料的价格为0.25元，所以整个包装盒外表面涂色的费用是0.25×108=27(元).

12. ★由几个相同的棱长为1的小正方体搭成的立体图形从上面看到的平面图形如图①所示,小正方形中的数字表示该位置上的小正方体的个数.
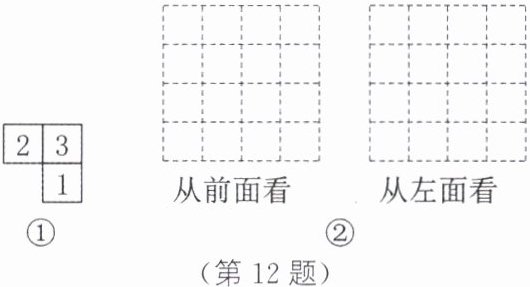
(1)请在如图②所示的网格中分别画出这个立体图形从前面、左面看到的平面图形.
(2)根据从三个不同方向看到的平面图形,可得这个立体图形的表面积(包括底面积)为______.
(3)若上述小正方体搭成的立体图形从上面看到的平面图形不变,在小正方体总个数不变、位置可以改变的前提下,搭成的不同的立体图形中,表面积(包括底面积)最大为多少？

答案：
（1）如图①所示.
（2）24.
（3）要使表面积最大，则需满足小正方体重合的面最少，此时从上面看到的平面图形如图②所示.这样从上面看共有3个小正方形，从左面看共有5个小正方形，从前面看共有5个小正方形，则该立体图形的表面积(包括底面积)为(3+5+5)×2=26.所以搭成的不同的立体图形中，表面积(包括底面积)最大为26.