第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
9. 新考法·阅读理解题(2025·重庆渝中期末)【阅读材料】
材料一:N 进制数与十进制数之间的转换.
将 N 进制数转化为十进制数时,只要将N 进制数的每个数字依次乘基数n的相应整数次幂,然后将这些乘积相加,就可得到与其相等的十进制数,规定:$a^{0}= 1(a≠0)$.例如:$(1302)_{5}= 1×5^{3}+3×5^{2}+0×5^{1}+2×$$5^{0}= 202.$
将十进制数转化为与其相等的 N 进制数,用十进制数除以基数n,然后将商继续除以n,直到商为0,将所得的余数按倒序从低位到高位排序即可.
例如,将89转化为五进制数:
因为$89÷5= 17... 4,17÷5= 3... 2,3÷5= 0... 3$,所以$89= (324)_{5}.$
材料二:二进制数加减运算的法则.
加法法则:$0+0= 0,0+1= 1,1+0= 1,1+1= 10.$
减法法则:$0-0= 0,0-1= -1,1-0= 1,10-1= 1$(同一数位不够减时,向高一位借1当2).
根据以上法则,二进制数的加减法可类比十进制数的竖式加法、减法规则进行运算.
$\begin{array}{r} (101)_{2}\\ +(10)_{2}\\ \hline (111)_{2}\end{array} $,$\begin{array}{r} (111)_{2}\\ +(10)_{2}\\ \hline (1001)_{2}\end{array} $
例如: ,
所以$(101)_{2}+(10)_{2}= (111)_{2},(111)_{2}+(10)_{2}= (1001)_{2}.$
$\begin{array}{r} (1111)_{2}\\ -(101)_{2}\\ \hline (1010)_{2}\end{array} $,$\begin{array}{r} (1101)_{2}\\ -(110)_{2}\\ \hline (111)_{2}\end{array} $
例如: ,
所以$(1111)_{2}-(101)_{2}= (1010)_{2},(1101)_{2}-(110)_{2}= (111)_{2}.$
【解决问题】
(1) 将六进制数$(251)_{6}$转化成十进制数,结果为______;将十进制数73转化成二进制数,结果为______.
(2) 计算(列竖式表示加减过程,结果用二进制数表示):
①$(1110)_{2}+(1011)_{2};$
②$(10110)_{2}-(1011)_{2}.$
(3) 探究二进制的乘法法则:
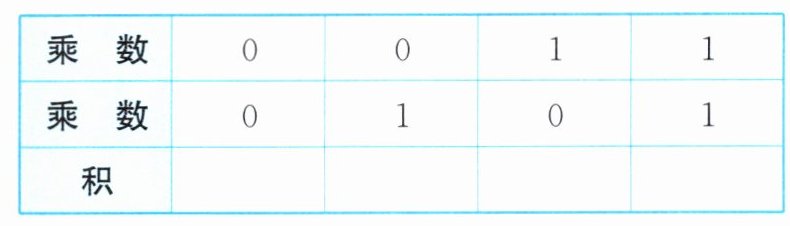
根据以上乘法法则,计算:$(1101)_{2}×(101)_{2}$(结果用二进制数表示).
材料一:N 进制数与十进制数之间的转换.
将 N 进制数转化为十进制数时,只要将N 进制数的每个数字依次乘基数n的相应整数次幂,然后将这些乘积相加,就可得到与其相等的十进制数,规定:$a^{0}= 1(a≠0)$.例如:$(1302)_{5}= 1×5^{3}+3×5^{2}+0×5^{1}+2×$$5^{0}= 202.$
将十进制数转化为与其相等的 N 进制数,用十进制数除以基数n,然后将商继续除以n,直到商为0,将所得的余数按倒序从低位到高位排序即可.
例如,将89转化为五进制数:
因为$89÷5= 17... 4,17÷5= 3... 2,3÷5= 0... 3$,所以$89= (324)_{5}.$
材料二:二进制数加减运算的法则.
加法法则:$0+0= 0,0+1= 1,1+0= 1,1+1= 10.$
减法法则:$0-0= 0,0-1= -1,1-0= 1,10-1= 1$(同一数位不够减时,向高一位借1当2).
根据以上法则,二进制数的加减法可类比十进制数的竖式加法、减法规则进行运算.
$\begin{array}{r} (101)_{2}\\ +(10)_{2}\\ \hline (111)_{2}\end{array} $,$\begin{array}{r} (111)_{2}\\ +(10)_{2}\\ \hline (1001)_{2}\end{array} $
例如: ,
所以$(101)_{2}+(10)_{2}= (111)_{2},(111)_{2}+(10)_{2}= (1001)_{2}.$
$\begin{array}{r} (1111)_{2}\\ -(101)_{2}\\ \hline (1010)_{2}\end{array} $,$\begin{array}{r} (1101)_{2}\\ -(110)_{2}\\ \hline (111)_{2}\end{array} $
例如: ,
所以$(1111)_{2}-(101)_{2}= (1010)_{2},(1101)_{2}-(110)_{2}= (111)_{2}.$
【解决问题】
(1) 将六进制数$(251)_{6}$转化成十进制数,结果为______;将十进制数73转化成二进制数,结果为______.
(2) 计算(列竖式表示加减过程,结果用二进制数表示):
①$(1110)_{2}+(1011)_{2};$
②$(10110)_{2}-(1011)_{2}.$
(3) 探究二进制的乘法法则:

根据以上乘法法则,计算:$(1101)_{2}×(101)_{2}$(结果用二进制数表示).
答案:
(1) 103;1001001. 解析:$(251)_{6}=2× 6^{2}+5× 6^{1}+1× 6^{0}=72 + 30 + 1 = 103$. $73÷ 2 = 36\cdots\cdots1$,$36÷ 2 = 18\cdots\cdots0$,$18÷ 2 = 9\cdots\cdots0$,$9÷ 2 = 4\cdots\cdots1$,$4÷ 2 = 2\cdots\cdots0$,$2÷ 2 = 1\cdots\cdots0$,$1÷ 2 = 0\cdots\cdots1$,
所以将十进制数73转化成二进制数,结果为1001001.
(2)①
所以$(1110)_{2}+(1011)_{2}=(11001)_{2}$.
②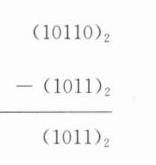
所以$(10110)_{2}-(1011)_{2}=(1011)_{2}$.
(3)由题意,填表如下: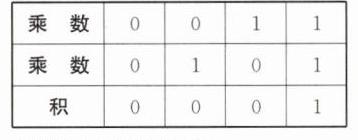
根据以上乘法法则,得
所以$(1101)_{2}×(101)_{2}=(1000001)_{2}$.
(1) 103;1001001. 解析:$(251)_{6}=2× 6^{2}+5× 6^{1}+1× 6^{0}=72 + 30 + 1 = 103$. $73÷ 2 = 36\cdots\cdots1$,$36÷ 2 = 18\cdots\cdots0$,$18÷ 2 = 9\cdots\cdots0$,$9÷ 2 = 4\cdots\cdots1$,$4÷ 2 = 2\cdots\cdots0$,$2÷ 2 = 1\cdots\cdots0$,$1÷ 2 = 0\cdots\cdots1$,
所以将十进制数73转化成二进制数,结果为1001001.
(2)①

所以$(1110)_{2}+(1011)_{2}=(11001)_{2}$.
②
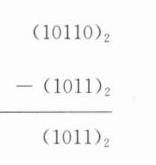
所以$(10110)_{2}-(1011)_{2}=(1011)_{2}$.
(3)由题意,填表如下:

根据以上乘法法则,得

所以$(1101)_{2}×(101)_{2}=(1000001)_{2}$.
查看更多完整答案,请扫码查看


