《2025年拔尖特训七年级数学上册人教版》

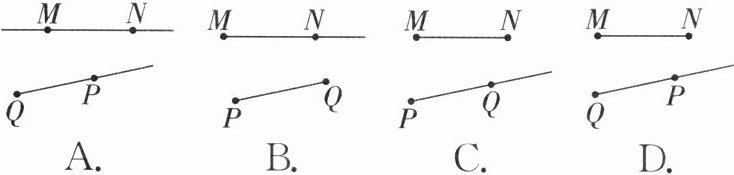
1. (2025·宿州萧县期末)下列各图中,表示线段 MN,射线 PQ 的是 (C)

答案： C

2. (2025·南通崇川期末)如图,下列说法中,不正确的是 (D)

A.直线 AB 与直线 BA 是同一条直线
B.线段 AB 与线段 BA 是同一条线段
C.射线 OA 与射线 OB 是同一条射线
D.射线 OA 与射线 AB 是同一条射线

答案： D

3. 四条直线相交,最多有 a 个交点,最少有 b 个交点,则 $10a + b= $______61.

答案： 61 解析:易知四条直线相交，最少有1个交点，最多有6个交点，所以a=6,b=1.所以10a+b=10×6+1=61.

4. (2025·宁波江北期末)观察图形,图中共有______条射线.

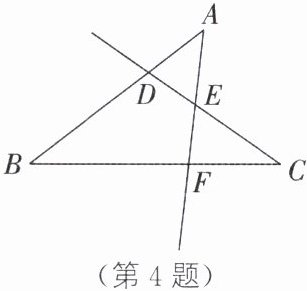
答案：
6 解析:如图，图中的射线有射线CE,射线ED,射线DM,射线AE,射线EF,射线FN,共6条.　　　

5. 如图,平面上有三个点 A,B,C.
(1)根据下列语句画图：作出射线 AC,CB,直线 AB；在射线 CB 上取一点 D(不与点 C 重合),使 $BD = BC$.
(2)用适当的语句表述点 D 与直线 AB 的位置关系：______.

答案：

(1)如图所示.
(2)点D在直线AB外(直线AB不经过点D).　　　　

6. (2024·唐山期末)平面上有 A,B,C 三点,如果 $AB = 10$,$AC = 6$,$BC = 4$,那么下列说法中,正确的是 ( )

A.点 C 在线段 AB 上
B.点 C 在线段 AB 的延长线上
C.点 C 在直线 AB 外
D.点 C 的位置无法确定

答案：
A 解析:因为AB=10,AC=6,BC=4,所以AB=AC+BC.所以点C在线段AB上，如图所示.所以选项A正确.　

7. 如图,棋盘上有黑、白两种颜色的棋子若干. 若直线 l 经过 3 枚颜色相同的棋子,则这样的直线共有3条.

答案： 3

8. 在平面内,2 条直线相交最多有 $a_{1}$ 个交点,3 条直线相交最多有 $a_{2}$ 个交点,4 条直线相交最多有 $a_{3}$ 个交点……以此类推,求 $\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+…+\frac{1}{a_{10}}$ 的值.
答案讲解

答案： 由于2条直线相交最多有1个交点，3条直线相交最多有(1+2)个交点，4条直线相交最多有(1+2+3)个交点……所以n条直线相交最多有(1+2+3+…+n-1)个交点，即$a_{n-1}=\frac{n(n-1)}{2}$(n为大于或等于2的整数).所以$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+\cdots+\frac{1}{a_{10}}=\frac{1}{\frac{2×1}{2}}+\frac{1}{\frac{3×2}{2}}+\frac{1}{\frac{4×3}{2}}+\cdots+\frac{1}{\frac{11×10}{2}}=\frac{2}{2×1}+\frac{2}{3×2}+\frac{2}{4×3}+\cdots+\frac{2}{11×10}=2×\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots+\frac{1}{10}-\frac{1}{11}\right)=2×\frac{10}{11}=\frac{20}{11}$.