《2025年拔尖特训七年级数学上册人教版》

11. 某同学在计算$-3\frac{7}{8}-N$时,误将“-N”看成了“+N”,从而算得结果是$5\frac{3}{4}$,则正确的结果是$-13\frac{1}{2}$.

答案： $-13\frac{1}{2}$ 解析:由题意,得$N=5\frac{3}{4}-(-3\frac{7}{8})=5\frac{3}{4}+3\frac{7}{8}=9\frac{5}{8}$.所以正确的结果是$-3\frac{7}{8}-9\frac{5}{8}=-13\frac{1}{2}$.

12. 已知M是-5的相反数与-12的绝对值的差,N是比-8大5的数.
(1)求M-N的值.
(2)求N-M的值.
(3)从(1)(2)的计算结果中,你能知道M-N与N-M之间有什么关系吗？

答案： （1）由题意,得$M=-(-5)-|-12|=5-12=-7$,$N=-8+5=-3$.所以$M-N=(-7)-(-3)=-4$.
（2）由（1）,得$N-M=(-3)-(-7)=-3+7=4$.
（3）因为$M-N+N-M=0$,所以$M-N$与$N-M$互为相反数.

13. 对于有理数a,b,n,d,如果|a-n|+|b-n|= d,那么称a和b关于n的“相对距离”为d.例如,|2-1|+|3-1|= 3,则2和3关于1的“相对距离”为3.
(1)-3和4关于1的“相对距离”为7.
(2)若a和5关于2的“相对距离”为6,求a的值.
由题意,得|a-2|+|5-2|=6,所以|a-2|+3=6.所以|a-2|=3.所以a-2=±3.所以a=5或-1.

答案： （1）7.
（2）由题意,得$|a-2|+|5-2|=6$,所以$|a-2|+3=6$.所以$|a-2|=3$.所以$a-2=\pm 3$.所以$a=5$或$-1$.

14. 请在如图所示的各个圆圈内填上适当的数,使每个圆圈里的数都等于与它相邻的两个数的和.

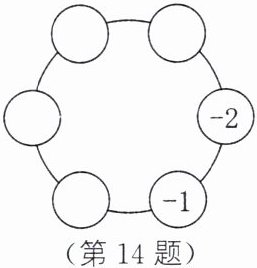
答案：
如图所示

15. 新考法·新定义题 定义一种新运算“△”：a△b= a-|b|,例如：3△(-2)= 3-|-2|= 3-2= 1.计算下列各式：
(1)(-2)△3.
(2)0△5.
(3)(-7)△(-6).
(4)[5△(-3)]△[3△(-1)].

答案： （1）原式$=(-2)-|3|=(-2)-3=-5$.
（2）原式$=0-|5|=0-5=-5$.
（3）原式$=(-7)-|-6|=(-7)-6=-13$.
（4）原式$=(5-|-3|)\triangle (3-|-1|)=(5-3)\triangle (3-1)=2\triangle 2=2-|2|=2-2=0$.