《2025年拔尖特训七年级数学上册人教版》

1. 将$(110101)_{2}$转化为十进制数为 (B)
A.106
B.53
C.55
D.108

答案： B 解析:$(110101)_{2}=1× 2^{5}+1× 2^{4}+0× 2^{3}+1× 2^{2}+0× 2^{1}+1× 2^{0}=32+16+4+1=53.$

2. 将十进制数91转化为二进制数.

答案： 因为$91=64+16+8+2+1=1× 2^{6}+0× 2^{5}+1× 2^{4}+1× 2^{3}+0× 2^{2}+1× 2^{1}+1× 2^{0},$所以十进制数 91 转化为二进制数应为 1011011.

3. (1)将$(331)_{5}$转化为十进制数.
(2)将$(46)_{7}$转化为十进制数.

答案：
(1)$(331)_{5}=3× 5^{2}+3× 5^{1}+1× 5^{0}=75+15+1=91.$
(2)$(46)_{7}=4× 7^{1}+6× 7^{0}=28+6=34.$

4. 将十进制数839转化为八进制数.

答案： $839=512+320+0+7=1× 8^{3}+5× 8^{2}+0× 8^{1}+7× 8^{0}=(1507)_{8}.$

5. 将十进制数193转化为九进制数.

答案： $193=162+27+4=2× 9^{2}+3× 9^{1}+4× 9^{0}=(234)_{9}.$

6. 计算机中常用的十六进制是满16进1的计数制,采用数字0～9和字母A～F共16个计数符号,关系如下表：

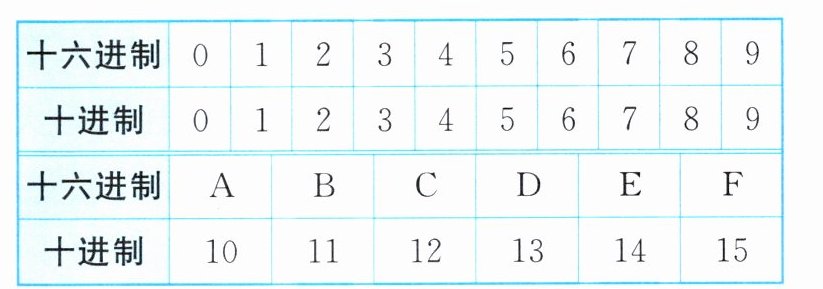
例如:十六进制数$71B= 7×16^2+1×16^1+11×16⁰= 1819,$即十六进制数71B相当于十进制数1819.试将十六进制数2E8转化为十进制数.

答案： $(2E8)_{16}=2× 16^{2}+14× 16^{1}+8× 16^{0}=2× 256+224+8=512+224+8=744.$