《2025年拔尖特训七年级数学上册人教版》

9. 若$P= \frac{1}{2}(x^{2}-y^{2}+3)$,$Q= \frac{1}{3}(x^{2}-2y^{2}+2)$,则$P$,$Q$的大小关系是 (A)
A.$P＞Q$
B.$P＜Q$
C.$P= Q$
D.无法确定

答案： A　解析:因为P=$\frac{1}{2}$(x²−y²+3),Q=$\frac{1}{3}$(x²−2y²+2),所以P−Q=$\frac{1}{2}$(x²−y²+3)−$\frac{1}{3}$(x²−2y²+2)=$\frac{1}{2}$x²−$\frac{1}{2}$y²+$\frac{3}{2}$−$\frac{1}{3}$x²+$\frac{2}{3}$y²−$\frac{2}{3}$=$\frac{1}{6}$x²+$\frac{1}{6}$y²+$\frac{5}{6}$＞0.所以P−Q＞0,即P＞Q.方法归纳：利用作差法比较两个数或两个式子的大小。若a−b＞0,则a＞b；若a−b=0,则a=b；若a−b＜0,则a＜b。运用作差法比较大小的一般步骤:
(1)作差；
(2)判断差的符号；
(3)确定大小关系。

10. (2024·德阳)若一个多项式加上$y^{2}+3xy-4$,结果是$3xy+2y^{2}-5$,则这个多项式为y²−1.

答案： y²−1　解析:由题意，得这个多项式为3xy+2y²−5−(y²+3xy−4)=3xy+2y²−5−y²−3xy+4=y²−1.

11. 已知轮船在静水中的速度为$(a+b)$km/h,它的逆流速度为$(2a-b)$km/h,则顺流速度为3bkm/h.

答案： 3b　解析:由题意，得顺流速度为(a+b)+[(a+b)−(2a−b)]=a+b+a+b−2a+b=3b(km/h).

12. 新情境·游戏活动 (2025·重庆江北期末)课外活动时,老师带着A,B,C三名同学玩游戏,首先,老师发给A,B,C三名同学相同数量的扑克牌(假定发到每名同学手中的扑克牌数量为$x$张,且数量足够多),然后,老师背对同学,让同学依次完成以下三个步骤:
第一步,A同学拿出3张扑克牌给B同学;
第二步,C同学拿出5张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.此时老师说:"B同学,你手中有11张扑克牌."大家一惊,觉得老师算得太快了.请你推演一下老师的话是否正确.

答案： 开始时，A,B,C三名同学有相同数量的扑克牌，均为x张。第一步后A同学手中扑克牌的张数为x−3,B同学手中扑克牌的张数为x+3,C同学手中扑克牌的张数为x；第二步后A同学手中扑克牌的张数为x−3,B同学手中扑克牌的张数为x+3+5,C同学手中扑克牌的张数为x−5；第三步后A同学手中扑克牌的张数为2(x−3),B同学手中扑克牌的张数为x+3+5−(x−3),C同学手中扑克牌的张数为x−5。所以B同学手中扑克牌的张数为x+3+5−(x−3)=x+3+5−x+3=11.所以老师的话是正确的。

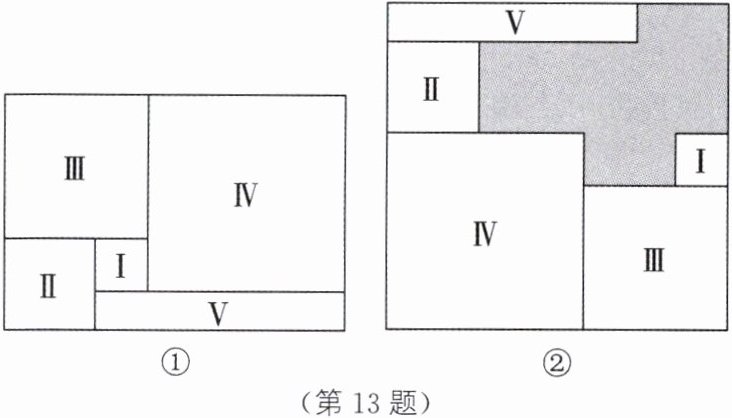
13. (2025·重庆江北期末)如图,将图①中周长为72的长方形纸片剪成Ⅰ,Ⅱ,Ⅲ,Ⅳ四个正方形和长方形Ⅴ,并将它们按图②的方式无重叠地放入另一个大长方形中,则涂色部分的周长为 (A)

A.54
B.52
C.46
D.45

答案： A　解析:设正方形I的边长为x,正方形II的边长为y，则正方形III 的边长为x+y,正方形IV的边长为2x+y,长方形V的长为3x+y,宽为y−x。如图,AB=2x+y+x+y−y=3x+y,BD=y−x+y+2x+y−(x+y)=2y.所以涂色部分的周长=2(AB+BD)=2(3x+y+2y)=6(x+y).因为题图①中大长方形的周长=2(3x+y+y+x+y+y)=8(x+y),即8(x+y)=72,所以x+y=9.所以6(x+y)=54.所以涂色部分的周长为54.

14. 已知$x$表示一个两位数,$y$表示一个三位数,现把$x放在y$的左边组成一个五位数,记为$A$;把$y放在x$的左边组成一个五位数,记为$B$.
(1)用含$x$,$y的代数式表示A-B$.
(2)$A-B$是9的倍数吗?为什么?
(3)已知一个三位数的百位上的数字为$m$,个位上的数字为$n$,把百位上的数字与个位上的数字交换位置,十位上的数字不变,原数与所得新数的差等于495,求$m-n$的值.

答案：
(1)由题意,得A=1000x+y,B=100y+x.所以A−B=(1000x+y)−(100y+x)=1000x+y−100y−x=999x−99y.
(2)A−B是9的倍数。由
(1)知,A−B=999x−99y=9(111x−11y),所以A−B是9的倍数。
(3)设十位上的数字是a.根据题意，可得原数=100m+10a+n,新数=100n+10a+m,两数之差为100m+10a+n−(100n+10a+m)=99m−99n.所以99m−99n=495.所以m−n=5.