《2025年拔尖特训七年级数学上册人教版》

10. 已知a为有理数,[a]表示不大于a的最大整数,如$[\frac{2}{5}]= 0$,$[1\frac{3}{4}]= 1$,$[-0.3]= -1$,$[-3\frac{1}{2}]= -4$,则计算$[-6\frac{5}{6}]-[5]×[-\frac{3}{4}]÷[4.9]$的结果是$-5\frac{3}{4}$.

答案： $-5\frac{3}{4}$ 解析:由题意，得原式$= -7 - 5×(-1)÷4 = -7 + 5÷4 = -7 + \frac{5}{4} = -5\frac{3}{4}$。

11. 数学老师布置了一道计算题：$(-\frac{1}{12})÷(\frac{1}{3}-\frac{5}{6})$.
小明仔细思考了一番,用了一种特殊的方法来解决这个问题.
小明的解答：
原式的倒数为$(\frac{1}{3}-\frac{5}{6})÷(-\frac{1}{12})= (\frac{1}{3}-\frac{5}{6})×(-12)= -4+10= 6$,
所以$(-\frac{1}{12})÷(\frac{1}{3}-\frac{5}{6})= \frac{1}{6}$.
(1)小明的解答是否正确？请说明理由.
(2)请你运用小明的方法计算：$(-\frac{1}{24})÷(\frac{1}{3}-\frac{1}{6}+\frac{3}{8})$.

答案：
(1)正确。理由:一个数的倒数的倒数等于原数。
(2)原式的倒数为$(\frac{1}{3} - \frac{1}{6} + \frac{3}{8})÷(-\frac{1}{24}) = (\frac{1}{3} - \frac{1}{6} + \frac{3}{8})×(-24) = -8 + 4 - 9 = -13$，所以$(-\frac{1}{24})÷(\frac{1}{3} - \frac{1}{6} + \frac{3}{8}) = -\frac{1}{13}$。

12. (2025·武汉武昌期末)给出下列说法：
① 若$a+b= 0$,则$\frac{a}{b}= -1$;② 若$a+b＜0$,且$\frac{b}{a}＞0$,则$|a+3b|= -a-3b$;③ 若$|a|＞|b|$,则$(a+b)(a-b)＞0$.其中,正确的有______(填序号).

答案：
②③ 解析:对于①，当$a = b = 0$时，$\frac{a}{b}$无意义。故①错误，不符合题意。对于②，因为$\frac{b}{a} ＞ 0$，所以a,b同号。因为$a + b ＜ 0$，所以$a ＜ 0$，$b ＜ 0$。所以$a + 3b ＜ 0$。所以$|a + 3b| = -a - 3b$。故②正确，符合题意。对于③，若$|a| ＞ |b|$，则有四种情况。$1^{\circ}$如图①，此时$a ＞ b ＞ 0$，所以$a + b ＞ 0$，$a - b ＞ 0$。所以$(a + b)(a - b) ＞ 0$。$2^{\circ}$如图②，此时$-a ＜ b ＜ 0 ＜ a$，所以$a + b ＞ 0$，$a - b ＞ 0$。所以$(a + b)(a - b) ＞ 0$。$3^{\circ}$如图③，此时$a ＜ b ＜ 0$，所以$a + b ＜ 0$，$a - b ＜ 0$。所以$(a + b)(a - b) ＞ 0$。$4^{\circ}$如图④，此时$a ＜ 0 ＜ b ＜ -a$，所以$a + b ＜ 0$，$a - b ＜ 0$。所以$(a + b)(a - b) ＞ 0$。综上所述，若$|a| ＞ |b|$，则$(a + b)(a - b) ＞ 0$。故③正确，符合题意。因此，正确的有②③。

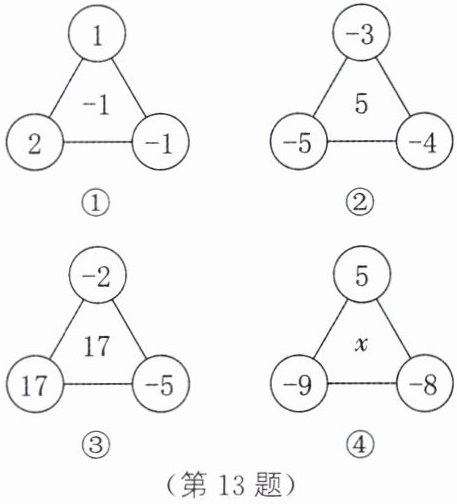
13. 观察图①～④所示的图形,解答问题：
(1)计算图①②③中三个角上的三个数的积,三个数的和,再计算三个数的积与和的商.
(2)请用你发现的规律求出图④中的数x的值.
]

答案：
(1)题图①:三个角上的三个数的积为$1×(-1)×2 = -2$，三个数的和为$1 + (-1) + 2 = 2$，积与和的商为$-2÷2 = -1$。题图②:三个角上的三个数的积为$(-3)×(-4)×(-5) = -60$，三个数的和为$(-3) + (-4) + (-5) = -12$，积与和的商为$(-60)÷(-12) = 5$。题图③:三个角上的三个数的积为$(-2)×(-5)×17 = 170$，三个数的和为$(-2) + (-5) + 17 = 10$，积与和的商为$170÷10 = 17$。
(2)$x = [5×(-8)×(-9)]÷[5 + (-8) + (-9)] = -30$。