《2025年拔尖特训七年级数学上册人教版》

4. 某商店销售某种品牌的电冰箱,其中某一型号的电冰箱每台的标价为a元,商店为了促销,将电冰箱一律按标价的八折销售,张先生购买一台该型号的电冰箱时又用了一张200元的代金券,则张先生实际支付的费用是(0.8a-200)元.

答案： (0.8a-200)

5. 按如图所示的运算程序,当输入$x= -3$,$y= 2$时,输出的结果是25.

答案： 25

6. (2024·渭南二模)某民族服饰的花边均是由若干个❀的基础图形组成的有规律的图案.如图,第1个图案由4个❀组成,第2个图案由7个❀组成,第3个图案由10个❀组成……按此规律排列下去,第2024个图案中❀的个数为______6073.

答案： 6 073 解析:观察题图可知,第1个图案由4个❀组成,即$4=1×3+1$,第2个图案由7个❀组成,即$7=2×3+1$,第3个图案由10个❀组成,即$10=3×3+1$……第n个图案中❀的个数为$3n+1$.所以第2 024个图案中❀的个数为$3×2024+1=6073$.

7. (2025·抚顺新宾期末)学校办公楼前有一块长为m、宽为n的长方形空地(如图),计划在其中心位置留出一个直径为2a的圆形区域建一个喷泉,两边分别规划一个长为b、宽为a的长方形休息区,涂色部分为绿地.

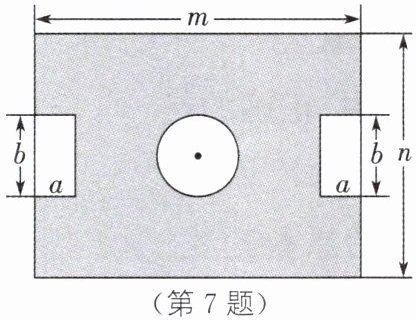
(1)用代数式表示涂色部分的面积(结果保留π).
(2)当$m= 8$,$n= 6$,$a= 1$,$b= 2$时,涂色部分的面积是多少(π取3)？

答案： （1）涂色部分的面积为$mn-2ab-πa^{2}$.
（2）当$m=8,n=6,a=1,b=2$时，涂色部分的面积为$8×6-2×1×2-π×1^{2}=48-4-π\approx 41$.

8. 如图所示为从左向右依次摆放序号分别为1,2,3,…,n的卡片,每张卡片上均画有若干个小圆点,其中任意相邻的4张卡片上的小圆点数量之和相等.

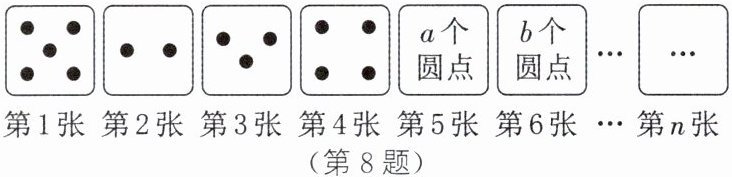
(1)分别求出a,b的值.
(2)当$n= 26$时,所有卡片上的小圆点数量之和是多少？
(3)小明说：“第99张卡片上的小圆点的个数是3.”请判断他的说法是否正确.

答案： （1）由题意,得$5+2+3+4=2+3+4+a,2+3+4+a=3+4+a+b$,解得$a=5,b=2$.
（2）由题意,得连续4张相邻的卡片上小圆点的个数之和为$5+2+3+4=14$.又因为$26÷4=6... 2$,所以$6×14+5+2=91$(个).所以所有卡片上的小圆点数量之和是91个.
（3）说法正确.因为卡片上小圆点的个数以5,2,3,4为一个循环反复出现,所以$99÷4=24... 3$.所以第99张卡片上的小圆点的个数是3.所以小明的说法正确.