《2025年拔尖特训七年级数学上册人教版》

14.(2025·济南历下期中改编)类比是运用过去的经验解决新问题的一种思维过程.
【回顾反思】
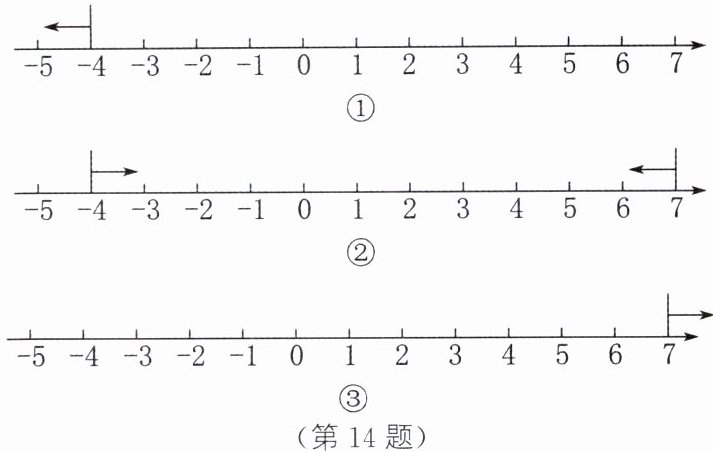
数学兴趣小组在研究$|x+4|+|x-7|$的最小值问题时,利用"一个数的绝对值就是这个数所对应的点到原点的距离"这一概念,发现$|x+4|$就是x和-4所对应的两个点之间的距离,$|x-7|$就是x和7所对应的两个点之间的距离.下列是同学们用-4和7这两个数所对应的点将数轴分为三个部分,然后分别在这三个部分上探究x对应的点到-4对应的点与x对应的点到7对应的点的距离之和,并运用数形结合的思想解决问题的过程:
① 如图①,若$x＜-4$,则在数轴上x对应的点到-4对应的点与x对应的点到7对应的点的距离之和大于11.② 如图②,若$-4＜x＜7$,则在数轴上x对应的点到-4对应的点与x对应的点到7对应的点的距离之和等于11.③ 如图③,若$x＞7$,则数轴上x对应的点到-4对应的点与x对应的点到7对应的点的距离之和大于11.④ 若$x= -4$,则在数轴上x对应的点到-4对应的点与x对应的点到7对应的点的距离之和等于11.⑤ 若$x= 7$,则x对应的点到-4对应的点与x对应的点到7对应的点的距离之和等于11.
综上所述,$|x+4|+|x-7|$的最小值为11.
【模仿应用】试仿照上面的方法,求$|a-6|+|a+3|$的最小值.

答案： 由题意,得①若$a ＜ -3$,则数轴上a对应的点到-3对应的点与a对应的点到6对应的点的距离之和大于9.②若$-3 ＜ a ＜ 6$,则数轴上a对应的点到-3对应的点与a对应的点到6对应的点的距离之和等于9.③若$a ＞ 6$,则数轴上a对应的点到-3对应的点与a对应的点到6对应的点的距离之和大于9.④若$a = -3$或$a = 6$,则数轴上a对应的点到-3对应的点与a对应的点到6对应的点的距离之和等于9. 综上所述，$|a - 6| + |a + 3|$的最小值为9.

15. 如图,M,N,P,R分别是数轴上四个整数所对应的点,其中有一个点是原点,并且点M与点N、点N与点P、点P与点R之间的距离均为1.数a对应的点在点M与点N之间,数b对应的点在点P与点R之间.若$|a|+|b|= 3$,则M,N,P,R这四个点中,表示原点的可能是哪个点?请说明理由.

答案： 表示原点的可能是点M或R.理由:由题意，得数a,b对应的点之间的距离小于3. 又因为$|a| + |b| = 3$, 所以原点不在数a,b对应的点之间.所以表示原点的可能是点M或R.