《2025年拔尖特训七年级数学上册人教版》

12. (2025·渭南蒲城期末)已知代数式$ 2x^{m}y^{2}-(n-3)x+1 $是关于x,y的三次二项式,求$ m^{2}+n $的值.

答案： 由题意可知，$m+2=3$，$n-3=0$，解得$m=1$，$n=3$.所以$m^{2}+n=1^{2}+3=4$.

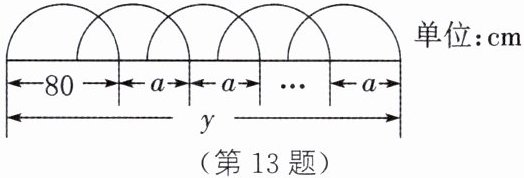
13. 如图,某花园的护栏是用一些半圆形钢条围成的,半圆的直径为80cm,且每增加1根半圆形钢条,护栏的长度就增加acm(a＞0).设半圆形钢条的总根数为x(x为正整数),护栏的总长度为ycm.
(1)当a= 60时,用含x的代数式表示y(结果要求化简).
(2)用含a,x的代数式表示y(结果要求化简),并求当a= 50,x= 41时y的值.

答案： （1）由题意，得$y=80+60(x-1)=60x+20$.（2）由题意，得$y=80+a(x-1)=ax+80-a$.当$a=50$，$x=41$时，$y=50×41+80-50=2080$.

14. 定义:f(a,b)是关于a,b的多项式,如果$ f(a,b)= f(b,a) $,那么f(a,b)叫作“对称多项式”.例如:若$ f(a,b)= a^{2}+a+b+b^{2} $,则$ f(b,a)= b^{2}+b+a+a^{2} $,显然,f(a,b)是“对称多项式”.
(1)试说明$ f(a,b)= a^{2}-2ab+b^{2} $是“对称多项式”.
因为$f(a,b)=a^{2}-2ab+b^{2}$，所以$f(b,a)=b^{2}-2ab+a^{2}$.所以$f(a,b)=f(b,a)$，即$f(a,b)=a^{2}-2ab+b^{2}$是“对称多项式”.
(2)请写出一个“对称多项式”:$ f(a,b)= $$a+b$(不多于四项).
(3)如果$ f_{1}(a,b) 和 f_{2}(b,a) $均为“对称多项式”,那么$ f_{1}(a,b)+f_{2}(a,b) $一定是“对称多项式”吗?如果一定是,请说明理由;如果不一定是,请举例加以说明.
不一定是.举例不唯一，如设$f_{1}(a,b)=a+b$，$f_{2}(b,a)=-b-a$，则$f_{1}(a,b)+f_{2}(a,b)=a+b+(-a-b)=0$，是单项式，不是多项式.所以$f_{1}(a,b)+f_{2}(a,b)$不一定是“对称多项式”.

答案： （1）因为$f(a,b)=a^{2}-2ab+b^{2}$，所以$f(b,a)=b^{2}-2ab+a^{2}$.所以$f(a,b)=f(b,a)$，即$f(a,b)=a^{2}-2ab+b^{2}$是“对称多项式”.（2）答案不唯一，如$a+b$.（3）不一定是.举例不唯一，如设$f_{1}(a,b)=a+b$，$f_{2}(b,a)=-b-a$，则$f_{1}(a,b)+f_{2}(a,b)=a+b+(-a-b)=0$，是单项式，不是多项式.所以$f_{1}(a,b)+f_{2}(a,b)$不一定是“对称多项式”.

15. 已知$ (a-1)x^{5}+x^{|b+2|}-2x^{2}+bx+b(b≠-2) $是关于x的二次三项式,求$ (a-b)^{2} $的值.

答案： 因为$(a-1)x^{5}+x^{|b+2|}-2x^{2}+bx+b(b≠-2)$是关于x的二次三项式，所以分情况讨论：① 当$a-1=0$时，解得$a=1$.（ⅰ）令$|b+2|=2$，得$b=0$或$b=-4$.当$b=0$时，原式$=-x^{2}$，不是关于x的二次三项式，舍去；当$b=-4$时，原式$=-x^{2}-4x-4$，是关于x的二次三项式，此时$(a-b)^{2}=[1-(-4)]^{2}=25$.（ⅱ）令$|b+2|=1$，得$b=-1$或$b=-3$.当$b=-1$时，原式$=-2x^{2}-1$，不是关于x的二次三项式，舍去；当$b=-3$时，原式$=-2x^{2}-2x-3$，是关于x的二次三项式，此时$(a-b)^{2}=[1-(-3)]^{2}=16$.② 当$a-1=-1$，且$|b+2|=5$，即$a=0$，$b=3$或$-7$时，原多项式为关于x的二次三项式，此时$(a-b)^{2}=(0-3)^{2}=9$或$(a-b)^{2}=[0-(-7)]^{2}=49$.综上所述，$(a-b)^{2}$的值为25或16或9或49.