《2025年拔尖特训七年级数学上册人教版》

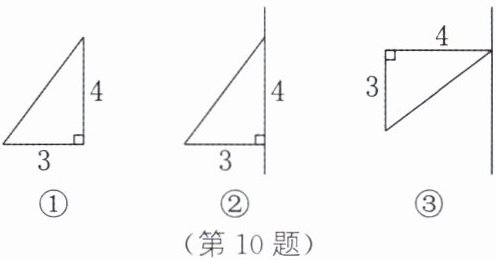
10. (2025·淄博期中)如图①所示为一个两直角边长分别为3,4的直角三角形. 旋转方式一：如图②,以边长为4的直角边所在直线为轴旋转一周,得到一个几何体. 旋转方式二：如图③,过边长为3的直角边所对的顶点且与边长为3的直角边平行的直线为轴旋转一周,得到另一个几何体. 试猜想哪种旋转方式得到的几何体的体积更大,并通过计算证明自己的猜想($V_{圆柱}= πr^{2}h$,$V_{圆锥}= \frac {1}{3}πr^{2}h$).
]

答案： 旋转方式二得到的几何体的体积更大.旋转方式一得到的几何体的体积为$\frac{1}{3}$π×3²×4 = 12π.旋转方式二得到的几何体的体积为π×4²×3 - $\frac{1}{3}$π×4²×3 = 32π.因为12π＜32π,所以旋转方式二得到的几何体的体积更大.

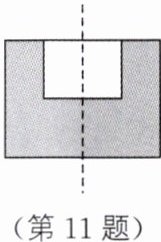
11. 如图,大长方形的长为8cm,宽为6cm,小长方形的长为4cm,宽为3cm,以长边中间的点的连线(图中的虚线)为轴,求图中涂色部分旋转一周得到的几何体的表面积.

答案： 由题意，可得大圆柱的侧面积为π×8×6 = 48π(cm²),小圆柱的侧面积为π×4×3 = 12π(cm²),大圆柱上下底面圆的面积为2π×($\frac{8}{2}$)² = 32π(cm²),所以几何体的表面积为48π + 12π + 32π = 92π(cm²).

12. 一把三角尺的两条直角边的长是6和8,斜边长是10,将这把三角尺绕着它的一边所在的直线旋转一周(温馨提示：$V_{圆柱}= πr^{2}h$,$V_{球体}= \frac {4}{3}πR^{3}$,$V_{圆锥}= \frac {1}{3}πr^{2}h$).
(1)绕着它的斜边所在的直线旋转一周形成的几何体是______.
(2)绕着它长为6的直角边所在的直线旋转一周形成的几何体的体积是多少？
(3)绕着斜边所在的直线旋转一周形成的几何体的体积与绕着长为8的直角边所在的直线旋转一周形成的几何体的体积哪个大？

答案：

(1)两个圆锥形成的几何体.
(2)绕着它长为6的直角边所在的直线旋转一周形成的几何体的体积是$\frac{1}{3}$π×8²×6 = 128π.
(3)如图，设斜边上的高为m.所以$\frac{1}{2}$×10m = $\frac{1}{2}$×6×8,解得m = $\frac{24}{5}$.所以绕着斜边所在的直线旋转一周形成的几何体的体积为$\frac{1}{3}$π×($\frac{24}{5}$)²×10 = 76.8π.绕着长为8的直角边所在的直线旋转一周形成的几何体的体积为$\frac{1}{3}$π×6²×8 = 96π.因为76.8π＜96π,所以绕着长为8的直角边所在的直线旋转一周形成的几何体的体积大.