《2025年拔尖特训七年级数学上册人教版》

1. 数学活动课上,李老师给出一组按一定规律排列的数:2,-4,8,-16,32,…第n个数是(D)
A.$2^{n}$
B.$-2^{n}$
C.$(-1)^{n}×2^{n}$
D.$(-1)^{n+1}×2^{n}$

答案： D

2. 有如下数列:$a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},... ,a_{n-2},a_{n-1},a_{n},...$,满足$a_{n-2}\cdot a_{n}= 2a_{n-1}$.若$a_{1}= 1,a_{3}= 4$,则$a_{2024}$的值为(D)
A.8
B.6
C.4
D.2

答案： D 解析:因为$a_{n-2}\cdot a_{n}= 2a_{n-1}$,所以$2a_{2}=a_{1}\cdot a_{3}$.又因为$a_{1}= 1,a_{3}= 4$,所以$a_{2}=2$.以此类推,$a_{4}=4$,$a_{5}=2$,$a_{6}=1$,$a_{7}=1$,$a_{8}=2$,…,由此可见,这列数以1,2,4,4,2,1为一个循环反复出现.又因为$2024÷6=337\cdots\cdots2$,所以$a_{2024}=2$.

3. 用围棋棋子按如图所示的规律摆图形,则摆第n个图形需要围棋棋子的枚数为(B)
A.$3n-2$
B.$3n+2$
C.$5n$
D.$5n-2$

答案： B 解析:由题图可知,摆第1个图形需要围棋棋子的枚数为$5=1×3+2$;摆第2个图形需要围棋棋子的枚数为$8=2×3+2$;摆第3个图形需要围棋棋子的枚数为$11=3×3+2$……所以摆第n个图形需要围棋棋子的枚数为$3n+2$.

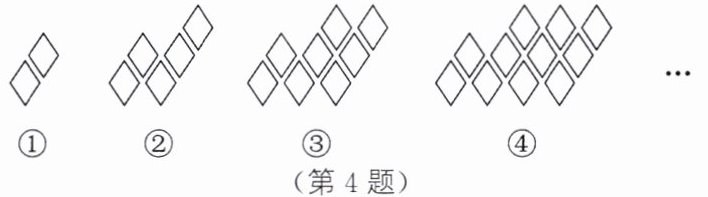
4. (2024·重庆B卷)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形……按此规律,则第⑧个图案中,菱形的个数为(C)
...
A.20
B.21
C.23
D.26

答案： C 解析:由题图可知,第①个图案中,菱形的个数为$2=1×3-1$;第②个图案中,菱形的个数为$5=2×3-1$;第③个图案中,菱形的个数为$8=3×3-1$;第④个图案中,菱形的个数为$11=4×3-1$……所以第ⓝ个图案中,菱形的个数为$3n-1$.当$n=8$时,$3n-1=23$,即第⑧个图案中,菱形的个数为23.

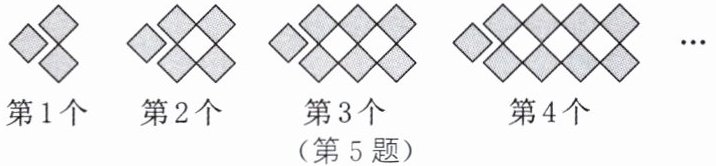
5. 如图所示的图形都是由同样大小的灰色正方形纸片组成的,其中第1个图形中有3张灰色正方形纸片,第2个图形中有5张灰色正方形纸片,第3个图形中有7张灰色正方形纸片,第4个图形中有9张灰色正方形纸片……按此规律排列下去,则第2024个图形中灰色正方形纸片的张数为(D)
...
A.4027
B.4047
C.4048
D.4049

答案： D 解析:由题意可知,第1个图形中有3张灰色正方形纸片,即$3=3+2×0$,第2个图形中有5张灰色正方形纸片,即$5=3+2×1$,第3个图形中有7张灰色正方形纸片,即$7=3+2×2$,第4个图形中有9张灰色正方形纸片,即$9=3+2×3$……所以第n个图形中灰色正方形纸片的张数为$3+2(n-1)=2n+1$.当$n=2024$时,$2×2024+1=4049$.

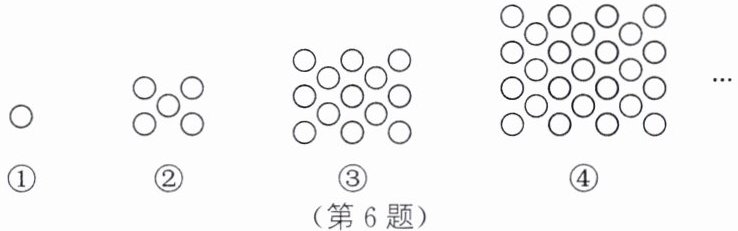
6. (2025·天津期中改编)如图所示为用圆圈拼成的图案,图①由1个圆圈组成,图②由5个圆圈组成,图③由13个圆圈组成,依此规律,图⑧由______个圆圈组成.
...

113

答案： 113 解析:由题意,得题图①由$1^{2}=1$(个)圆圈组成,题图②由$2^{2}+1^{2}=5$(个)圆圈组成,题图③由$3^{2}+2^{2}=13$(个)圆圈组成,…依此规律,题图ⓝ由$[n^{2}+(n-1)^{2}]$个圆圈组成,所以题图⑧由$8^{2}+7^{2}=113$(个)圆圈组成.

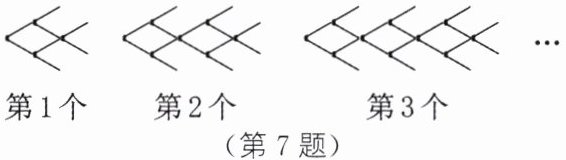
7. 如图所示为一组有规律的图案组成的“小鱼”群,它由若干根火柴棒组成.第1个图案由8根火柴棒组成,第2个图案由14根火柴棒组成,第3个图案由20根火柴棒组成,第4个图案由26根火柴棒组成……按此规律,第n个图案由多少根火柴棒组成(用含n的代数式表示)?
...

答案： 根据题意,得第1个图案由$6×1+2=8$(根)火柴棒组成,第2个图案由$6×2+2=14$(根)火柴棒组成,第3个图案由$6×3+2=20$(根)火柴棒组成,第4个图案由$6×4+2=26$(根)火柴棒组成……所以第n个图案由$(6n+2)$根火柴棒组成.