《2025年拔尖特训七年级数学上册人教版》

1.(2025·徐州市沛县期末)如果a 和 2024 互为相反数,那么a 表示的数是 (A)
A.-2024
B.$\frac{1}{2024}$
C.2024
D.$-\frac{1}{2024}$

答案： A

2. 有下列各组数：-1 与$-(-1)$,$-(+2)$与-2,$\frac{1}{5}与-(+\frac{1}{5})$,$-(-12)$与 12,$-(+3)与-(-3)$.其中,互为相反数的有 (D)
A.0 组
B.1 组
C.2 组
D.3 组

答案： D

3.(2025·惠州期末)若$x+1$的相反数是-7,则$x= $6.

答案： 6

4. 如图,在数轴上,一个单位长度表示 1.
(1)若点 A,D 表示的数互为相反数,则点 D 表示的数为2.5.
(2)若点 B,F 表示的数互为相反数,则点 E 表示的数的相反数为-2.
]

答案：
(1) 2.5
(2) -2

5. 在如图所示的数轴上表示下列各数及它们的相反数.
0,-2.5,-3,+5,$1\frac{1}{3}$,4.5.
]

答案：
在数轴上表示如图所示.

6. 数轴上表示数a 和数b 的两点之间的距离为6.若a 的相反数是2,则b 的值是 (D)
A.4
B.-4
C.-8
D.4 或-8

答案： D

7. 如果a 表示某个有理数,那么下列说法中,正确的是 (D )
A.+a 和$-(-a)$互为相反数
B.+a 和-a 一定不相等
C.-a 一定是负数
D.$-(+a)和+(-a)$一定相等

答案： D　解析：+a和-(-a)相等，故选项A错误. 当a = 0时，+a = -a = 0，故选项B错误. 当a = 0时，-a = 0，-a不是负数，故选项C错误，-(+a) = +(-a) = -a，故选项D正确.

8. 若-m 与$-(-2025)$互为相反数,则m 的值为2025.

答案： 2025

9. -5.1 和它的相反数之间的整数的个数是11.

答案： 11

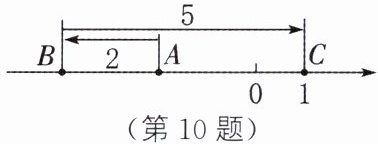
10. 如图,数轴上一动点 A 沿数轴向左移动 2 个单位长度到达点 B,再沿数轴向右移动 5 个单位长度到达点 C,则与点 A 表示的数互为相反数的数是2.
]

答案： 2　解析：因为数轴上一动点A向左移动2个单位长度到达点B，再向右移动5个单位长度到达点C，点C表示的数为1，所以点B表示的数为 -4. 所以点A表示的数为 -2. 所以与点A表示的数互为相反数的数是2.

11. 在数轴上,点 A,B 表示的数互为相反数,且两点之间的距离是 12,点 A 沿着数轴先向右运动 2 秒,再向左运动 5 秒到达点 C 的位置.设点 A 的运动速度为每秒 1.5 个单位长度,则点 C 表示的数的相反数为-1.5或10.5.

答案： -1.5或10.5　解析：因为点A，B表示的数互为相反数，且两点之间的距离是12，所以点A表示的数为6或 -6. 因为点A运动的距离为1.5×(5 - 2) = 4.5，且点C在点A的左侧，所以点C在数轴上表示的数为1.5或 -10.5. 所以点C表示的数的相反数是 -1.5或10.5.

12.(1)计算下列各式：
① $-(-2)$.
② $+(-\frac{1}{5})$.
③ $-[-(-4)]$.
④ $-[-(+3.5)]$.
⑤ $-\{-[-(-5)]\}$.
⑥ $-\{-[-(+5)]\}$.
(2)当+5 的前面有 2025 个负号时,化简后的结果是多少？
(3)当-5 的前面有 2026 个负号时,化简后的结果是多少？你能总结出什么规律？

答案：
(1) ① -(-2) = 2.② $+(-\frac{1}{5}) = -\frac{1}{5}$.③ $-[-(-4)] = -4$.④ $-[-(+3.5)] = 3.5$.⑤ $-\{-[-(-5)]\} = 5$.⑥ $-\{-[-(+5)]\} = -5$.
(2) 当 +5的前面有2025个负号时，化简后的结果是 -5.
(3) 当 -5的前面有2026个负号时，化简后的结果是 -5.规律：若在一个数的前面有偶数个负号，则化简后的结果是其本身；若在一个数的前面有奇数个负号，则化简后的结果是这个数的相反数.