《2025年拔尖特训七年级数学上册人教版》

1. (2024·漯河期末)如图,数轴上A,B两点对应的数分别为-8和12,点P从原点O出发,以每秒1个单位长度的速度沿数轴的负方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴的正方向运动,设运动时间为t秒.当AP= BQ时,t的值为$\frac{20}{3}$或4.

答案： $\frac{20}{3}$或4 解析:因为点A表示的数为-8,点B表示的数为12,所以$AP=|-t-(-8)|=|8-t|$,$BQ=|2t-12|$.因为$AP=BQ$,所以$|8-t|=|2t-12|$,即$8-t=2t-12$或$t-8=2t-12$,解得$t=\frac{20}{3}$或$t=4$.所以当$AP=BQ$时,t的值为$\frac{20}{3}$或4.

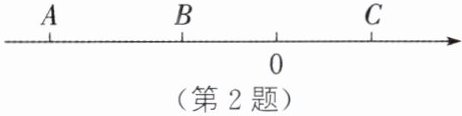
2. 如图,数轴上有A,B,C三个点,点A,B,C对应的数分别是a,b,c,且满足|a+24|+|b+10|$+(c-10)^2= 0,$动点P从点A出发,以每秒1个单位长度的速度向终点C运动.
(1)求a,b的值.
(2)若点P到点A的距离是点P到点B的距离的2倍,求点P对应的数.
(3)当点P运动到点B时,点Q从点A出发,以每秒3个单位长度的速度向点C运动,点Q到达点C后,再立即以同样的速度返回,运动到终点A.设点Q的运动时间为m秒,当m为何值时,P,Q两点之间的距离为4?

答案：
(1)因为$|a+24|+|b+10|+(c-10)^2=0$,所以$a+24=0$,$b+10=0$,$c-10=0$,解得$a=-24$,$b=-10$,$c=10$.
(2)A,B两点之间的距离为$-10-(-24)=14$.
①当点P在点A,B之间时,$AP=14×\frac{2}{2+1}=\frac{28}{3}$.所以点P对应的数是$-24+\frac{28}{3}=-\frac{44}{3}$.
②当点P在点B,C之间时,$AP=14×2=28$.所以点P对应的数是$-24+28=4$.综上所述,点P对应的数是$-\frac{44}{3}$或4.
(3)若点Q从点A向点C运动,则当点P在点Q的右侧,且点Q还没追上点P时,$3m+4=14+m$,解得$m=5$.当点P在点Q的左侧,且点Q追上点P时,$3m-4=14+m$,解得$m=9$.若点Q从点C向点A运动,则当点P在点Q的左侧时,$14+m+4+3m-34=34$,解得$m=12.5$.当点P在点Q的右侧时,$14+m-4+3m-34=34$,解得$m=14.5$.综上所述,当m的值为5或9或12.5或14.5时,P,Q两点之间的距离为4.

3. (2024·泰州期末)数轴是重要的数学学习工具,利用数轴可以将数与形完美结合.已知结论:数轴上点A,B表示的数分别为a,b,则A,B两点之间的距离AB= |a-b|;线段AB的中间点表示的数为$\frac{a+b}{2}$.
(1)若点A,B表示的数分别为a,b,a与$-\frac{1}{5}$互为倒数,b与-7互为相反数,则A,B两点之间的距离为12;线段AB的中间点表示的数为1.
(2)在(1)的条件下,动点P从点A出发以每秒3个单位长度的速度沿数轴向左运动,动点Q从点B出发以每秒5个单位长度的速度沿数轴向左运动,M是线段PQ的中间点.设运动时间为t秒.
①点M表示的数为1-4t(用含t的代数式表示).
②在运动过程中,A,P,Q中恰有一点是连接另外两点所得线段的中间点,求t的值.
易知点P在数轴上表示的数为$-5-3t$,点Q在数轴上表示的数为$7-5t$.当P为线段AQ的中间点时,则$2(-5-3t)=7-5t-5$,解得$t=-12$(不合题意,舍去).当A为线段PQ的中间点时,则$2×(-5)=-5-3t+7-5t$,解得$t=1.5$.当Q为线段PA的中间点时,则$2×(7-5t)=-5-3t-5$,解得$t=\frac{24}{7}$.综上所述,t的值为1.5或$\frac{24}{7}$.
③线段PQ,AM的长度随时间t的变化而变化,当点Q在点P的左侧时,是否存在常数m,使mPQ+AM的值为定值?若存在,求常数m及该定值;若不存在,请说明理由.
存在.当点Q在点P的左侧时,$PQ=-5-3t-(7-5t)=2t-12$,$AM=-5-(1-4t)=4t-6$,所以$mPQ+AM=m(2t-12)+4t-6=(2m+4)t-12m-6$.所以当$2m+4=0$,即$m=-2$时,$mPQ+AM$的值为定值.此时$mPQ+AM=-12×(-2)-6=18$.所以$m=-2$,定值为18.

答案：
(1)12;1.
(2)①$1-4t$.
②易知点P在数轴上表示的数为$-5-3t$,点Q在数轴上表示的数为$7-5t$.当P为线段AQ的中间点时,则$2(-5-3t)=7-5t-5$,解得$t=-12$(不合题意,舍去).当A为线段PQ的中间点时,则$2×(-5)=-5-3t+7-5t$,解得$t=1.5$.当Q为线段PA的中间点时,则$2×(7-5t)=-5-3t-5$,解得$t=\frac{24}{7}$.综上所述,t的值为1.5或$\frac{24}{7}$.
③存在.当点Q在点P的左侧时,$PQ=-5-3t-(7-5t)=2t-12$,$AM=-5-(1-4t)=4t-6$,所以$mPQ+AM=m(2t-12)+4t-6=(2m+4)t-12m-6$.所以当$2m+4=0$,即$m=-2$时,$mPQ+AM$的值为定值.此时$mPQ+AM=-12×(-2)-6=18$.所以$m=-2$,定值为18.