《2025年启东中学作业本八年级数学上册苏科版连淮专版》

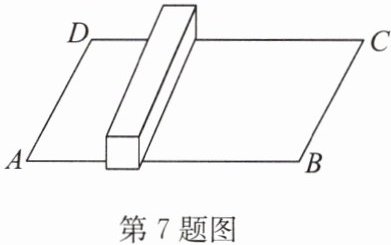
7.(2024·湖滨新区期末)如图,在一个长为20米,宽为18米的矩形草地上,放着一根长方体木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2米的正方形,一只蚂蚁从点A处,爬过木块到达C处需要走的最短路程是______米.

30

答案： 30

8.(2024·灌南县期中)葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是24 cm,当一段葛藤绕树干盘旋1圈升高18 cm时,这段葛藤的长是30cm.

答案： 30

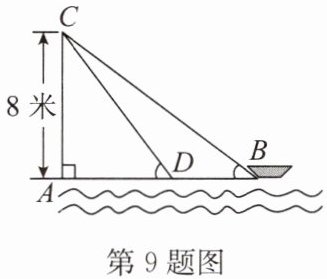
9.(2024·灌南县期中)如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,几分钟后船到达点D的位置,此时绳子CD的长为10米,问船向岸边移动了多少米?

答案： 解:
∵在Rt△ABC中,∠CAB=90°,BC=17米,AC=8米,
∴AB= $\sqrt{BC²−AC²}$=$\sqrt{17²−8²}$=15(米).
∵在Rt△ACD中,CD=10米,
∴AD= $\sqrt{CD²−AC²}$=$\sqrt{10²−8²}$=6(米).
∴BD=AB−AD=15−6=9(米).
答:船向岸边移动了9米.

10.(2024·海州区期中)某广场视野开阔,阻挡物少,成为不少市民放风筝的最佳场所.某校八年级的小明和小亮两位同学在学习了勾股定理之后,为了测得风筝的垂直高度CE,他们进行了如下操作:①测得BD的长度为8米(注:$BD\perp CE$);②根据手中剩余线的长度计算出风筝线BC的长为17米;③牵线放风筝的小明身高1.6米.
(1)求风筝的垂直高度CE;
(2)若小明同学想让风筝沿CD方向下降9米,则他应该往回收线多少米?

答案：
解:
(1)在Rt△CDB中,由勾股定理,得CD²=BC² - BD²=17²−8²=225,
∴CD=15(负值舍去),
∴CE=CD+DE=15+1.6=16.6(米).
答:风筝的高度CE为16.6米.
(2)如答图,CD=15,在CD上取点M,使CM=9,连接BM.由题意，得CM=9米,则DM=6米，

∴BM=$\sqrt{DM^{2}+BD^{2}}$=$\sqrt{6²+8²}$=10(米),
∴BC−BM=17−10=7(米).
答:他应该往回收线7米.

11.情境创新类问题(2024·清江浦区期末)如图,笔直的河流一侧有一旅游地C,河边有两个漂流点A,B,其中$AB= BC$,由于某种原因,由C到B的路现在已经不通,为方便游客,相关部门决定在河边新建一个漂流点H(点A,H,B在同一条直线上),并新修一条路CH,测得$AC= \sqrt{5}$千米,$CH= 2$千米,$AH= 1$千米.
(1)判断$\triangle BCH$的形状,并说明理由;
(2)求原路线BC的长.

答案： 解:
(1)△BCH是直角三角形.理由如下:
∵AC=$\sqrt{5}$千米,CH=2千米,AH=1千米，
∴AH²+CH²=AC²,
∴△ACH是直角三角形,∠AHC=90°.
∵点A,H,B在同一条直线上，
∴∠BHC=180°−∠AHC=90°,
∴△BCH是直角三角形.
(2)设原路线BC的长为x千米,则AB=x千米,BH=(x - 1)千米.
在Rt△BCH中,由勾股定理,得(x - 1)²+2²=x²,解得x=2.5,
∴原路线BC的长为2.5千米.